10 consejos para la solución de problemas de razonamiento matemático GED y comprobar sus respuestas

Cuando usted está tomando el examen de GED Razonamiento Matemático (o alguna de las pruebas de GED para el caso), hay que luchar contra el reloj. A continuación se presentan diez consejos útiles para ahorrar tiempo y asegúrese de que las respuestas se llega a son los correctos.

• Ser realistas: Trate de desarrollar un sexto sentido sobre el mundo real alrededor de usted. Coches no obtienen 160 millas por galón, a menos que estén rodando cuesta abajo, así que si su respuesta es fuera de sintonía con la realidad, es probablemente equivocado. A menos que su prueba fue escrito por un genio maligno, las preguntas de la vida real deben tener alguna relación con la vida real como usted lo sepa. Si usted viene con una respuesta que parece extraño, compruebe si ha utilizado la conversión correcta. Por ejemplo, si una habitación 10-x-15-pies tiene un techo de 120 pies, es posible que tenga los pies por error convertidos a pulgadas.

• Ir con la conversión más fácil: Al leer la pregunta, prestar mucha atención a las unidades de medida. Las unidades en la cuestión deben ser uniformes y en relación con las unidades necesarias para la respuesta. Si todas las unidades están en pies y la pregunta pide una respuesta en pulgadas, usted sabe que usted tiene que convertir pies a pulgadas. Pero ¿qué hacer si algunas de las opciones de respuesta están en los pies y otros están en pulgadas?

  Si usted tiene que convertir unidades, seleccione la unidad con la menor posibilidad de producir un error y la mejor oportunidad de la estimación de la respuesta. Si una habitación mide 13-x-7 yardas, y la respuesta está en los pies, estos números son fáciles de multiplicar por 3 en la cabeza. Si la habitación es 12.48 yardas de largo, que sería mejor usar una calculadora y convertir al final. Los números enteros son más fáciles de trabajar que las fracciones o decimales.

• Multiplique por centenas, decenas y unidades: Al multiplicar un gran número por un pequeño uno (número de una o de dos dígitos), romper el gran número hacia abajo en sus partes componentes, multiplicar las partes por el número más pequeño, y añadir los resultados, como en el siguiente ejemplo:

  89 x 9 = (80 x 9) + (9 x 9) = 720 + 81 = 801

• Vueltas y estimación: Si las opciones de respuesta que tiene que elegir entre muy diferentes en magnitud, es posible que pueda elegir la respuesta correcta sin necesidad de calcular la respuesta exacta. Cuando se recibe una pregunta que implica la adición o sustracción, estimar los números con una precisión de 5 o 10 y hacer los cálculos en su cabeza. Adición de números que terminan en 5 o 0 es más fácil de agregar los números que terminan en 3 o 7, por ejemplo.

  Si la pregunta especifica un valor máximo, redondo todo hasta determinar rápidamente si el total es menor que el valor máximo, como en este ejemplo:

  María está haciendo algunas compras rápido y no quiere gastar más de $ 20.00. Ella compra algunas manzanas de $ 5.73, algunas uvas para $ 4.77, y el lápiz labial de $ 6.73, más impuestos del 8%. ¿Ella mantenerse dentro de su presupuesto?

  Ronda todos los valores hasta el dólar más cercano y se ve que $ 6 + $ 5 + $ 7 = $ 18. Si el impuesto es del 8%, redondear hasta el 10%, y usted verá rápidamente que el impuesto sobre $ 18 sería de $ 1,80. $ 18 + $ 1.80 = $ 19.80, que es todavía menos de $ 20, así que usted sabe que María se mantuvo dentro de su presupuesto.

  Si la pregunta especifica un valor mínimo, redondo todos los demás valores abajo primero y luego realizar sus cálculos.

• Saltar y volver a las preguntas increíblemente duros: Tenga en cuenta que muchos matemáticos son gente perezosa que tratan de resolver los problemas de la forma más fácil posible. Si una pregunta es cada vez imposiblemente difícil de resolver, algo que suele ser mal. Compruebe sobre su trabajo y asegurarse de que ha copiado todos los números correctamente y que no ha utilizado la operación incorrecta en el trabajo a través del problema.

• Simplificar antes de hacer los cálculos: Antes de siquiera pensar en multiplicar o dividir fracciones o la realización de cualquier serie de operaciones matemáticas, considere si puede simplificar la ecuación antes de hacer los cálculos. Por simplificar, usted termina con menos y más pequeños números e incluso puede ser capaz de hacer los cálculos en su cabeza, ahorrándose preciosos minutos en la prueba. Por ejemplo, sin simplificar,

  

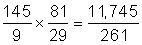
  pero si a simplificar,

  

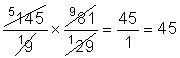
• Reste el porcentaje de descuento de uno: Si el problema le ofrece un descuento del 15% del precio regular, usted puede multiplicar ya sea el precio normal por 0,15 para calcular el descuento y restar esa cantidad del precio normal, o puede imaginar que si usted está recibiendo un 15% descuento, usted está pagando el 85% del precio normal, porque

  100% - 15% = 85%.

  En vez de hacer el problema en dos etapas, lo haces en una y se ahorrará unos segundos: multiplicar la cantidad por 0,85 para obtener los mismos resultados en un solo paso. También reduce sus posibilidades de hacer una error- los más pasos que das, más posibilidades tienen de cometer un error, especialmente cuando estás en un apuro.

• Estimar fracciones como cero, medio, o uno: Al trabajar con fracciones que son menos de uno, pregúntese si la fracción es más cercano a cero, medio, o uno, y luego estimar su respuesta. Aquí hay un par de ejemplos:

  

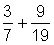
  Debido a que ambas fracciones están cerca de

  

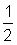
  la respuesta es cercano a 1.

  

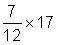
  Debido a que la fracción es poco más de

  

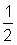
  la respuesta es probable que sea un poco más de la mitad de 17, o ligeramente más de 8,5.

• Añadir el impuesto o porcentaje de propina a uno: Al calcular el impuesto o la punta de un total, se puede calcular el impuesto o la punta y añadirlo al total (dos pasos) o añadir el porcentaje del impuesto o la punta al 100% y que se multiplican por el total (un paso). Por ejemplo, para salir de su servidor de un 15% de propina en un restaurante, se puede multiplicar la cantidad en el cheque por 0,15 y agregar esto a la cuenta para obtener la cantidad que usted debe dejar el servidor en total. O usted puede multiplicar el cheque por 1,15 para calcular la punta, más total (total 100% más el 15% de propina es 115% o 1.15). Una vez más, menos pasos y menos posibilidades de error, sobre todo si se utiliza el cálculo mental.

• Dibuja cartas y dados rollo: Muchos de los problemas de probabilidad implican cartas y dados, así que saber que una baraja tiene 52 cartas, 4 palos (diamantes, corazones, tréboles y picas), y 13 cartas de cada palo: ace, 02.10, sota, caballo y rey . Si usted quiere saber sus posibilidades de sacar un as de corazones de una baraja completa de tarjetas, usted sabe que una cubierta completa tiene 52 tarjetas y sólo el 1 as de corazones, por lo que las probabilidades son de 1 en 52 de sacar un as de corazones. Si usted es feliz simplemente dibujar cualquier as, a continuación, la cubierta todavía tiene 52 cartas, pero 4 ases, por lo que sus posibilidades de sacar un as son 4 en el 52, o 2 en 26, o 1 de cada 13.

  Preguntas dados también son comunes en la prueba. Tenga en cuenta que cada mueren (singular para " dados ") tiene 6 caras, numeradas del 1 al 6. Cada vez que lanzas un dado, usted tiene un 1 en 6 posibilidad de que se va a la tierra con un cierto número hacia arriba.