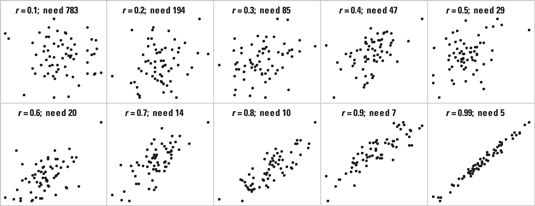
Para una prueba de correlación en bioestadística (como el de Pearson o el test de Spearman), escoger el gráfico de dispersión que se parece a una cantidad importante de correlación. Cada gráfico muestra el valor de r
(el coeficiente de correlación) y el número requerido de sujetos analizables (cada uno proporcionando una
X y un
y valor). Por ejemplo, si el gráfico de dispersión en la esquina inferior izquierda (correspondiente a
r = 0.6) parece mostrar una cantidad importante de correlación, necesitará unos 20 sujetos analizables.
Por otra r valores que no están en los gráficos de dispersión anteriores, utilizan esta regla de oro para estimar el tamaño de la muestra: Usted necesita unos 8 /r2 - 3 sujetos analizables.
Estimación Tamaño de la muestra de t Student para datos independientes Pruebas en Bioestadística
En bioestadística, al comparar las medias de dos grupos independientes de los sujetos usando una prueba t de Student no apareado, la tamaño del efecto se expresa como la relación de # 916- (delta, la diferencia entre las medias de dos grupos) dividido por # 963- (sigma, el intragrupal desviación estándar).
Cada gráfico en la figura siguiente se muestra la superposición de las curvas de la campana que indican la cantidad de separación entre dos grupos, junto con el tamaño del efecto (# 916 - / # 963-) y el número necesario de sujetos analizables en cada grupo. Elija la tabla que se parece a una cantidad importante de separación entre los dos grupos. Por ejemplo, si el gráfico medio (que corresponde a una diferencia entre grupos que es tres cuartas partes del tamaño de la desviación estándar dentro del grupo) se parece a una cantidad importante de la separación, entonces usted necesita cerca de 29 sujetos analizables por grupo (para un total de 58 sujetos analizables).

Por otra # 916 - / # 963- valores, utilice esta regla de oro para estimar el tamaño de la muestra: Se necesita alrededor de 16 / (# 916 - / # 963-)2 sujetos analizables en cada grupo.
Estimación Tamaño de la muestra de t pareada Estudiantes Pruebas en Bioestadística
En bioestadística, al comparar las mediciones pareadas (tales como los cambios entre dos puntos de tiempo para el mismo tema) utilizando una prueba t de Student apareado, la tamaño del efecto se expresa como la relación de # 916- (delta, el cambio medio) dividido por # 963- (sigma, la desviación estándar de los cambios). Otra quizás más fácil, manera, para expresar el tamaño del efecto es por el número relativo de los sujetos esperados con positivas frente a cambios negativos. (Estas relaciones se muestran debajo de cada curva.)
Cada gráfico en la siguiente figura muestra una curva de campana que indica la propagación de cambios, junto con el tamaño del efecto (# 916 - / # 963-), la proporción de positivos a las diferencias negativas, y el número necesario de sujetos analizables (cada tema proporcionando un par de mediciones). Elija la tabla que se parece a una cantidad importante de cambio (con respecto a la línea vertical que representa ningún cambio). Por ejemplo, el gráfico medio corresponde a un cambio medio que es tres cuartas partes tan grande como la desviación estándar de los cambios, con cerca de 3,4 veces como muchos temas creciente como decreciente. Si esto se parece a una cantidad importante de cambio, entonces usted necesita 16 pares de mediciones (por ejemplo, 16 sujetos, cada uno con un pretratamiento y un valor de post-tratamiento).

Por otra # 916 - / # 963- valores, utilice esta regla de oro para estimar el tamaño de la muestra: Usted necesita unos 8 / (# 916 - / # 963-)2 + 2 pares de mediciones.
Estimación Tamaño de la muestra al comparar dos proporciones en Bioestadística
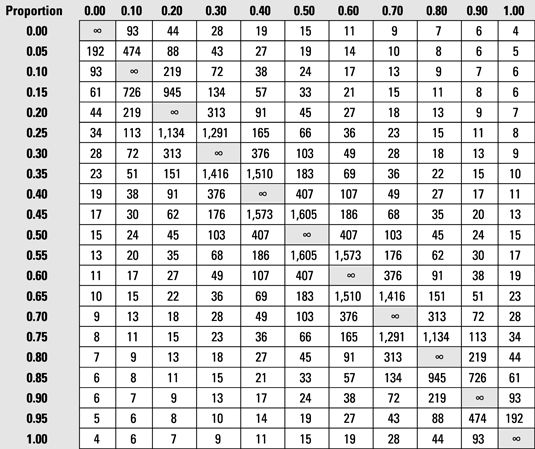
La proporción de sujetos que tienen algún atributo (como respuesta al tratamiento) se puede comparar entre dos grupos de sujetos mediante la creación de una tabla de referencias cruzadas de los datos, donde las dos filas representan los dos grupos, y las dos columnas representan la presencia o ausencia del atributo. En bioestadística, esta tabla de referencias cruzadas se puede analizar con una prueba exacta de chi cuadrado o de Fisher.
Para estimar el tamaño de la muestra requerida, es necesario proporcionar las proporciones esperadas en los dos grupos. Busque las dos proporciones que desea comparar a la izquierda y la parte superior de la tabla siguiente. (No importa qué proporción se mira de qué lado.) El número en la celda de la tabla es el número de sujetos analizables que necesita en cada grupo. (El tamaño total de muestra requerido es el doble de este número.)
Por ejemplo, si usted espera que 40 por ciento de los sujetos no tratados con una determinada enfermedad para morir, pero sólo el 30 por ciento de los sujetos tratados con un nuevo fármaco para morir, se encontraría la celda en la intersección de la fila de 0.30 y la columna de 0,40 (o vice versa), que contiene el número 376. Por lo que necesita 376 sujetos analizables en cada grupo, o 752 sujetos analizables en total.