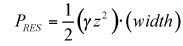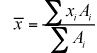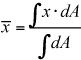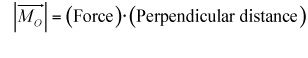Solución de problemas de estática pueden ser complicated- cada problema requiere una lista de elementos para tener en cuenta y ecuaciones para crear y resolver. Resolver problemas de estática con facilidad mediante el uso de esta lista:
Dibuje un diagrama de cuerpo libre de todo el sistema.
Además de las dimensiones y ángulos, debe incluir cuatro categorías principales de elementos en un diagrama de cuerpo libre correctamente construido:
Cargas externas aplicadas
Cargas internas Revealed
Reacciones de apoyo
Peso propio
Escribe ecuaciones de equilibrio para calcular tantas reacciones de apoyo desconocida como sea posible.
Para solucionar para las fuerzas internas, identificar el tipo de estructura y escribir sus ecuaciones de equilibrio.
Después de identificar el tipo de estructura, entonces sabe qué técnica utilizar para ayudarle a escribir sus ecuaciones de equilibrio:
Trincheras / miembros axiales: Los miembros se cargan con sólo fuerzas axiales interna. Para resolver, se puede utilizar el método de los nudos o el método de las secciones.
Vigas (miembros de flexión): Los miembros están cargados de fuerzas internas axiales, fuerzas cortantes y momentos. Para resolver, cortar el miembro en el lugar deseado, dibuje un nuevo diagrama de cuerpo libre de la sección de corte, y escribir ecuaciones de equilibrio.
Marcos / máquinas: Los miembros están cargados de fuerzas internas axiales, fuerzas cortantes y momentos. Para resolver, utilice el-lo-todo-apart golpe enfoque para romper la estructura en pedazos más pequeños. Busque bisagras internas como lugares comunes para separar su estructura y dibujar diagramas de cuerpo libre de resolver para las fuerzas de pines de conexión.
Estructuras de cable: Los miembros se construyen a partir de cables cargados axialmente. Identificar el tipo de carga por cable (concentrado, parabólica / uniforme o catenaria). Calcular la tensión del cable en el lugar de sag máxima conocida (o viceversa).
Superficies sumergidas: Los miembros están sometidos a la presión del fluido. Para resolver, dibuja un diagrama de cuerpo libre del diagrama de presión hidrostática, que es cero en la superficie del fluido y aumenta linealmente con la profundidad. Incluyen el peso del fluido sobre objetos con caras no verticales.
Estática: Informática Presiones superficie sumergida
Al trabajar los problemas superficiales sumergidos en la estática, recuerda que todas las superficies sumergidas tienen un fluido que actúa sobre ellos, haciendo presión. Usted debe calcular dos presiones: la resultante presión hidrostática y el peso propio fluido.
Resultante de presión hidrostática: La presión hidrostática resultante actúa horizontalmente a 0.333z (z es la profundidad del líquido) de la parte inferior de la distribución de la presión.
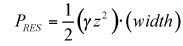
Fluid peso propio: El peso propio fluido es
actuando hacia abajo en el centroide (centro geométrico) de la zona de líquido.
Cálculo de una Región o en el Centro de Carga de Área: centroides
los centroide o centro de la zona de una región geométrica es el centro geométrico de la forma de un objeto. Centroide cálculos son muy comunes en la estática, ya sea que el cálculo de la ubicación de la resultante de una carga distribuida o determinar el centro de un objeto de masa. Para calcular el centro del área de una región (o carga distribuida), se puede calcular la X-coordenada (y las otras coordenadas de manera similar) a partir de las siguientes ecuaciones:
Por regiones discretas: Puede romper regiones discretas en formas simples, tales como triángulos, rectángulos, círculos, y así sucesivamente.
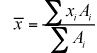
Para formas discretas, la creación de una tabla sencilla como la que sigue para cada coordenada puede ser útil. Puedes crear tantas filas como sea necesario para tantas regiones como usted tiene.
Tabla de la muestra para el cálculo de centroides para las Regiones discretos | Xyo | LAyo | XyoLAyo |
|---|
| Región 1 | x distancia para la Región 1 | Área de la Región 1 | Producto de xyo y unyo |
| TOTALES | ----------------- | Suma de todos los Ayo filas | Suma de todos los xyoLAyo filas |
Estática: Desarrollo de fuerza cortante y momento Diagramas
Diagramas de fuerza cortante y momento son una herramienta estática que los ingenieros crean para determinar la fuerza cortante interna y momentos en todos los lugares dentro de un objeto. Comience por la localización de los puntos críticos y luego dibujar el diagrama de corte.
Iniciar y detener de estructura (extremos)
Fuerzas concentradas
Momentos concentrados
Iniciar y detener de cargas distribuidas
Bisagras internas
Los sitios de apoyo
Puntos de cizalla cero (V = 0) - para diagramas de momento solamente.
Características importantes a tener en cuenta al elaborar el diagrama:
Fuerzas concentradas causan un salto inmediato en cizalla.
Momentos concentradas causan un salto instante en el momento.
Solicitar aumentos de carga para esquilar a momento (es decir, diagrama primera orden de carga, segunda cizalla orden, tercera momento orden).
La pendiente del diagrama de momento es igual al valor de la cizalladura.
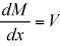
Si la zona de carga es positiva, el cambio en la cizalla es positivo. Si el área de cizallamiento es positivo, el cambio en el momento es positivo.
Fórmulas Vector cartesianas para Resolver Problemas Estática
En muchos problemas de estática, debe ser capaz de crear de forma rápida y eficiente vectores en el plano cartesiano. Afortunadamente, usted puede lograr sus creaciones vectoriales cartesianas fácilmente con las fórmulas vectoriales prácticos de esta lista:
Vectores de fuerza y vectores distancia son los vectores más básicas que tratar.
Estática: Cómo calcular Momento de una Fuerza
En la estática, moments son efectos (de una fuerza) que causan la rotación. Cuando se calcula el equilibrio, debe ser capaz de calcular un momento de cada fuerza en su diagrama de cuerpo libre. Para determinar momento de una fuerza, utiliza uno de dos cálculos diferentes, como se puede ver en la siguiente lista.
Cálculo escalar (de dos dimensiones): Para calcular el momento alrededor de un punto O en los cálculos escalares, que necesita la magnitud de la fuerza y la distancia perpendicular desde el punto O a la línea de acción de la Fuerza F.
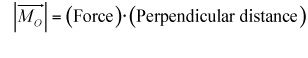
Cálculo vectorial (para dos o tres dimensiones): Para calcular el vector momento acerca de un punto O en los cálculos vectoriales, debe determinar la Fuerza F en forma vectorial cartesiana y el vector de posición del punto O a la línea de acción de la Fuerza F.
La fuerza es un vector
La fricción en superficies inclinadas en problemas de física
Cómo fricción se refiere a la fuerza normal
Cómo fricción estática impide el movimiento
Cómo calcular par perpendicular a la que se aplica la fuerza
Cómo dibujar diagramas de cuerpo libre de la física
Fricción cinética junto rampas
Física i practico problemas para los maniquíes
Ecuaciones de la física y las fórmulas
Estática: cizalla desarrollo y momento diagramas
La fricción estática a lo largo de las rampas