La teoría de cuerdas y la electrodinámica cuántica

Aunque los principios de la electrodinámica cuántica fueron elaborados por tres individuos, el más famoso fundador de QED era innegablemente Richard P. Feynman. Feynman fue igual de bueno en las matemáticas y la explicación de una teoría, lo que resultó en su creación de Diagramas de Feynman - una representación visual de las matemáticas que se encendió en QED.

Richard Phillips Feynman es uno de los personajes más interesantes de la física del siglo 20, de fácil clasificación con Einstein en la personalidad, si no en la fama pura. Al principio de su carrera, Feynman tomó la decisión consciente para trabajar solamente en los problemas que encontró interesante, algo que sin duda le sirvió bien. Afortunadamente para el mundo de la física, uno de estos problemas era la electrodinámica cuántica.

Debido a que el electromagnetismo es una teoría de campo, el resultado de QED era un teoría cuántica de campos - una teoría cuántica que contiene un valor en cada punto en el espacio. Usted puede imaginar que las matemáticas de tal teoría era intimidante, por decir lo menos, incluso para aquellos entrenados en la física y las matemáticas.

Feynman fue brillante, no sólo con la teoría física y las matemáticas, sino también con la explicación. Una forma que simplifica las cosas era a través de la aplicación de sus diagramas de Feynman. Aunque las matemáticas todavía era compleja, los diagramas significaba que podría empezar a hablar de la física sin necesidad de toda la complejidad de las ecuaciones. Y cuando lo hizo necesitará los números reales, los diagramas ayudaron a organizar sus cálculos.

En esta figura, se puede ver un diagrama de Feynman de dos electrones se aproximan entre sí. El diagrama de Feynman se encuentra en un espacio de Minkowski, que representa a los acontecimientos en el espacio-tiempo. Los electrones son las líneas continuas (llamados propagadores), Y a medida que cerca el uno al otro, se intercambia un fotón (el propagador serpenteante) entre los dos electrones.

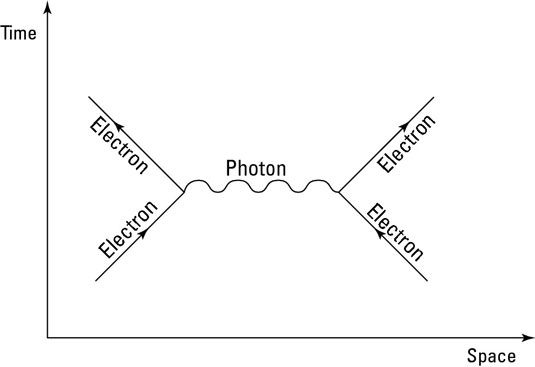
En otras palabras, en QED dos partículas comunican su información electromagnética emitiendo y absorbiendo un fotón. Un fotón que actúa de esta manera se llama fotón virtual o una fotón mensajero, porque se creó con el único fin de intercambiar esta información.

Esta fue la idea clave de QED, porque sin este intercambio de un fotón, no había manera de explicar cómo se comunicó la información entre los dos electrones.

También (y tal vez más importante desde el punto de vista de la física), una teoría cuántica de campos (al menos aquellos que parecen coincidir con nuestro mundo real) alcanza rápidamente el infinito si las distancias se hacen demasiado pequeña. Para ver cómo pueden surgir estos infinitos, tenga en cuenta tanto el hecho de que las fuerzas electromagnéticas se hacen más grandes a pequeñas distancias (infinitamente más grande a infinitamente pequeñas distancias) y también la distancia y el impulso de la relación del principio de incertidumbre de la mecánica cuántica.

Incluso hablar de los casos en los que dos electrones son muy cercanos entre sí (por ejemplo, dentro de una longitud de Planck) se convierte en prácticamente imposible en un mundo gobernado por la física cuántica.

Por electromagnetismo de cuantificación, como lo hace QED, Feynman, Schwinger y Tomonaga fueron capaces de utilizar la teoría a pesar de estos infinitos. Los infinitos todavía estaban presentes, sino porque el fotón virtual significa que los electrones no tienen que estar tan cerca uno del otro, no había tantos infinitos, y los que se quedaron no entró predicciones físicas.

Feynman, Schwinger y Tomonaga tomaron una teoría infinita y obtuvieron predicciones finitos. Una de las principales motivaciones para la unidad de desarrollar una teoría de cuerdas éxito es ir más allá y conseguir una teoría realidad finita.

El proceso matemático de la eliminación de los infinitos se llama renormalización. Este es un conjunto de técnicas matemáticas que se pueden aplicar para proporcionar un límite muy cuidadosamente definido para el continuo de valores contenidos en el campo.

En lugar de sumar todos los términos infinitos en el cálculo y obtener un resultado infinito, los físicos han descubierto que la aplicación de renormalización les permite redefinir los parámetros dentro de la suma por lo que se suma a una cantidad finita!

Sin la introducción de renormalización, los valores vuelven infinitas, y desde luego que no observan estos infinitos en la naturaleza. Con renormalización, sin embargo, los físicos obtienen predicciones inequívocas que se encuentran entre los resultados más precisos y mejor probados en toda la ciencia.