Estrategias de Ley para sumar y restar matrices
Para la prueba ACT de matemáticas, que debe de saber cómo trabajar con matrices. Afortunadamente, suma y resta de matrices son ambas operaciones simples y similares.
LA matriz es una cuadrícula de números o variables dispuestas en filas horizontales y columnas verticales.
La figura muestra una variedad de matrices.
Las dimensiones de las matrices (es decir, el número de filas y columnas) en la figura se
respectivamente. Por convención, el número de filas se indica primero y el número de columnas segundos.
Adición de matrices es fácil: Sólo tiene que añadir pares de números correspondientes en la matriz y colocar los resultados en una nueva matriz.
Las dos matrices que estás agregando deben tener dimensiones horizontales y verticales idénticas. Como resultado, la nueva matriz siempre tiene las mismas dimensiones que las dos matrices que estás agregando.
Ejemplo 1
¿Cuál de los siguientes es el resultado cuando se agrega
y
Para encontrar la respuesta correcta, sólo tiene que añadir cada par de números correspondientes
y luego colocarlos en las mismas posiciones en una nueva matriz. La respuesta correcta es la opción (C).
Restando matrices es similar a la adición de ellos: Para cada par de números correspondientes en la matriz, resta el segundo número de la primera y luego colocar los resultados en una nueva matriz. Como con la adición, sólo se puede restar una matriz de otra si ambas matrices tienen dimensiones horizontales y verticales idénticas.
Ejemplo 2
¿Cuál de los siguientes es el resultado cuando se realiza esta sustracción matriz:
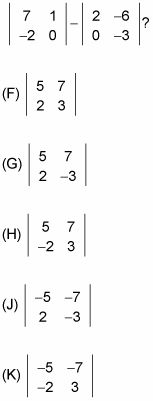
Restar cada par de números correspondientes a fin
y luego colocarlos en las mismas posiciones en una nueva matriz. La respuesta correcta es la opción (H).
Cómo utilizar las operaciones normales en una matriz en la r Probablemente la característica más fuerte de R es su capacidad para hacer frente a operaciones con matrices complejas de una manera fácil y optimizado. Debido a que gran parte de las estadísticas se reduce a operaciones con matrices, es natural…
Copie una matriz a otra en la TI-83 Plus Hay varias situaciones en las que es posible que desee copiar el contenido de una matriz a otra en la TI-83 Plus calculadora gráfica. Una de ellas es cuando se quiere definir una nueva matriz mediante la adición de filas y columnas de una matriz…
Editar, la pantalla y aumentar matrices en la TI-83 Plus Después de haber definido las matrices en la TI-83 Plus calculadora gráfica, puede que tenga que editarlos, mostrarlos en la pantalla de inicio, o añadir una matriz a otra. La calculadora le permite definir hasta diez matrices. Cada matriz puede…
¿Cómo definir una matriz en la TI-83 Plus Puede definir hasta diez matrices en la TI-83 Plus calculadora gráfica. Cada matriz puede tener unas dimensiones de hasta 99 X 99 y sólo puede contener las entradas de números reales.Para definir una matriz, siga estos pasos:prensapara entrar en…
Realizar operaciones aritméticas de la matriz en la TI-83 Plus Al evaluar expresiones aritméticas que implican matrices en la calculadora TI-3 Plus gráfica, normalmente se quiere realizar las siguientes operaciones básicas: la multiplicación escalar, negación (inverso aditivo), suma, resta, multiplicación…
Cómo introducir y almacenar matrices en la TI-84 Plus Puede introducir y almacenar matrices en la TI-84 Plus calculadora. LA matriz es una matriz rectangular de números dispuestos en filas y columnas. Las dimensiones, RXC, de una matriz se definen por el número de filas y columnas en la matriz. Los…
Aritmética Matrix en la TI-84 Plus calculadora Puede utilizar la TI-84 Plus calculadora para realizar operaciones aritméticas matriz. Al evaluar expresiones aritméticas que implican matrices, normalmente se quiere realizar las siguientes operaciones básicas: escalar multiplicación, suma,…
Cómo aplicar las operaciones básicas de matrices Al aplicar las operaciones básicas de matrices, funciona muy parecido a operar en múltiples términos dentro parentheses- sólo hay más términos en los "paréntesis" para trabajar. Al igual que con las operaciones sobre los números, un cierto…
Cómo multiplicar matrices uno por el otro Multiplicando las matrices es muy útil cuando resolver sistemas de ecuaciones. Esto es porque se puede multiplicar una matriz por su inversa en ambos lados del signo igual para obtener finalmente la matriz variable en un lado y la solución para el…
Reglas para sumar y restar matrices Para agregar o restar matrices, hay que operar en sus correspondientes elementos. En otras palabras, se añaden o se quitan la primera fila / primera columna en una matriz hacia o desde el mismo elemento exacta en otra matriz. Las dos matrices deben…
Matrices de dimensiones superiores para colecciones de números Arrays bidimensionales pueden ser considerados como la descripción de las tablas de valores, con filas y columnas (como un bloque de celdas en una hoja de cálculo), e incluso las matrices de dimensiones superiores pueden ser considerados como la…
Messing con preguntas de la matriz en la prueba de matemáticas acto De vez en cuando el acto puede deslizarse un problema matriz en la Prueba de Matemáticas. Si usted ve uno, no se asuste. Son fáciles de tratar al revisar el enfoque.Una matriz es simplemente un conjunto de valores. Aunque se pueden realizar varias…