Las estrategias para responder a las preguntas de opción múltiple en el acto

Si tiene problemas para resolver una cuestión ACT de matemáticas, puede aplicar diferentes estrategias con las opciones de respuesta dados para ayudarle a determinar qué opción es la correcta. La sección de matemáticas del ACT se compone de 60 preguntas de opción múltiple. Cada pregunta tiene cinco posibles respuestas. Todas las preguntas de opción múltiple que da un poco de información extra, porque usted sabe la respuesta correcta debe ser una de las cinco opciones dadas. Siempre tome un momento para notar estas opciones de respuesta, ya que pueden guiarlo a medida que trabaja en la solución del problema.

El siguiente ejemplo muestra cómo se puede confiar en las opciones de respuesta para resolver correctamente un problema.

Ejemplo 1

Si j² - 14j + 48 = 0, ¿cuál de los siguientes espectáculos todas de los posibles valores de j?

(A) -6

(B) 8

(C) 6, 8

(D) -6, 8

(E) -6, -8

Puede resolver la ecuación j² - 14j + 48 = 0 por factorización. En este caso, todos los valores en cada una de las cinco respuestas incluye 6 o 8 (más o un signo menos), por lo que tiene una ventaja en el factoring:

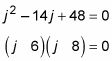
En este punto, sólo tiene que rellenar los signos (+ o -) dentro de los paréntesis. Debido a que 48 en la ecuación original es positivo, los dos signos deben ser los mismos (ya sea tanto + o ambos -). Y debido a -14 es negativo, por lo menos uno de los signos es negativo. Por lo tanto, ambos signos son negativos:

Ahora se puede resolver esta ecuación dividiéndola en dos ecuaciones separadas:

Por lo tanto, la respuesta correcta es la opción (C).

Preguntas de opción múltiple también le dan la oportunidad de llegar a la respuesta correcta mediante la conexión de las opciones de respuesta y solución. Tenga en cuenta que enchufar respuestas puede ser un poco de tiempo de consumo, por lo que si se puede encontrar una mejor manera de resolver el problema, vaya para él. Pero cuando te quedas atascado, esta táctica le da la oportunidad de responder a las preguntas que realmente no está seguro de cómo resolver. Considere el siguiente ejemplo.

(A) 4

(B) 5

(C) 6

(D) 7

(E) 8

Usted puede o no puede saber cómo resolver este tipo de ecuación. Y en todo caso, la resolución que puede llevar mucho tiempo. Así que usted puede tratar de conectar cada respuesta posible X para ver cuál funciona. Comience con Choice (A) y enchufe 4 para X:

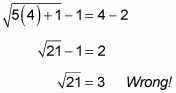
Esta opción de respuesta es obviamente erróneo, porque 21 no es un número cuadrado. Por Consiguiente,

es irracional y no es igual a 3. De hecho, esta opción de respuesta equivocada puede sugerir una manera de ahorrar aún más tiempo: La razón por la que esta respuesta está mal es que el valor de

evalúa a un número irracional, que estropea la ecuación. Así

tiene que ser un número racional, lo que significa 5x + 1 debe ser un número cuadrado. Intente probar opciones (B) a (E) de esta manera, teniendo en cuenta que usted está buscando un valor de X que hace 5X + 1 un número cuadrado:

Sólo un valor produce un número cuadrado, por lo que la respuesta correcta es la opción (D). Usted puede verificar esto mediante la conexión de 7 de X:

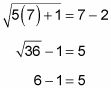
Algunas preguntas que piden el mayor o menor número que tiene una determinada propiedad. Estas preguntas proporcionan una gran oportunidad para poner a prueba las respuestas de forma individual hasta encontrar la correcta. Considere las siguientes estrategias:

• Al buscar el valor más bajo o menos, comenzar con el número más bajo y su forma de trabajo.

• En la búsqueda de la mayor o mayor valor, comenzar con el mayor número y su forma de trabajo.

El siguiente ejemplo ilustra esta estrategia.

Ejemplo 2

¿Cuál es el mínimo común denominador al añadir tres fracciones con denominadores de 6, 9 y 16?

(F) 60

(G) 120

(H) 144

(J) 240

(K) 288

Debido a que usted está buscando el mínimo común denominador, se puede encontrar la respuesta correcta probando números y descartar las respuestas incorrectas, empezando por el número más bajo.

Comience por la prueba para ver si el 60 es divisible por 6, 9 y 16:

Así Choice (F) es incorrecta. Ahora probar 120:

Así Choice (G) también está mal. A continuación, prueba de 144:

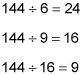
Así Choice (H) es la respuesta correcta. Por cierto, observe que 288 también es divisible por los tres denominadores. Sin embargo, Choice (K) es incorrecta porque la pregunta pide el mínimo común denominador, que es por qué comenzó conectando los números más bajos primero.