Ir fuera de la norma con las estadísticas no paramétricas
Todas las pruebas estadísticas se obtienen sobre la base de algunos supuestos sobre los datos, y la mayoría de las pruebas de significación clásicos (como las pruebas de la t de Student, análisis de varianza y pruebas de regresión) asumen que sus datos se distribuye de acuerdo con alguna distribución de frecuencias clásica ( más comúnmente la distribución normal).
Debido a que las funciones de distribución clásicos están escritas como expresiones matemáticas que involucran parámetros (como medios y desviación estándar), se llaman paramétrico funciones de distribución, y las pruebas que asumen sus datos se ajusta a una función de distribución paramétrica se llaman pruebas paramétricas. Debido a que la distribución normal es la distribución estadística más común, el término parlaprueba de métrica se utiliza más a menudo en el sentido de una prueba que asume los datos distribuidos normalmente.
Pero a veces los datos no es paramétrico. Por ejemplo, puede que no quiera asumir que sus datos se distribuyen normalmente, ya que puede ser muy notablemente sesgada, como se muestra en la parte A de la figura.
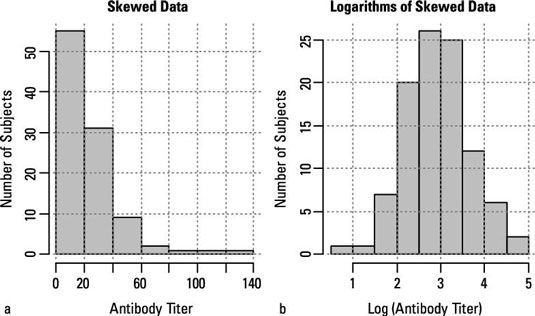
A veces, puede ser capaz de realizar algún tipo de transformación de sus datos para que sea distribuido con mayor normalidad. Por ejemplo, muchas variables que tienen una distribución asimétrica se pueden convertir en números distribuidos normalmente tomando logaritmos, como se muestra en la parte b. Si, por ensayo y error, puede encontrar algún tipo de transformación que normaliza sus datos, puede ejecutar las pruebas clásicas de los datos transformados.
Pero a veces los datos son tercamente anormal, y no se puede utilizar las pruebas paramétricas. Afortunadamente, los estadísticos han desarrollado pruebas especiales que no asumen una distribución normal de datos estos son (como es lógico) denominan pruebas no paramétricas. La mayor parte de las pruebas paramétricas clásicas comunes tienen contrapartes no paramétricas.
Como se puede esperar, las pruebas más conocidas y utilizadas no paramétricas son las que corresponden a los ensayos más conocidos y utilizados clásicos.
| Prueba paramétrico clásico | Equivalente no paramétrica |
|---|---|
| Un grupo o emparejado prueba t de Student | Regístrate Test- prueba de Wilcoxon firmado filas- |
| De dos grupo de prueba t de Student | Exámenes prueba de Wilcoxon de suma de rangos de Mann-Whitney |
| Utilizó un modelo lineal | Prueba de Kruskal-Wallis |
| Prueba de correlación de Pearson | Prueba de correlación de Spearman Rango |
La mayoría de las pruebas no paramétricas implican primero ordenar los valores de los datos, de menor a mayor, y registrar el rango de cada medición (el valor más bajo tiene un rango de 1, el siguiente valor más alto de un rango de 2, y así sucesivamente). Todos los cálculos subsiguientes se realizan con estas filas en lugar de con los valores de datos reales.
Aunque las pruebas no paramétricas no asumen la normalidad, ellos hacen ciertas suposiciones acerca de sus datos. Por ejemplo, muchas pruebas no paramétricas asumir que usted no tiene ningún valor atadas en el conjunto de datos (en otras palabras, no hay dos temas tienen exactamente los mismos valores). La mayoría de las pruebas paramétricas incorporan ajustes para la presencia de lazos, pero esto debilita la prueba y hace que los resultados no exacta.
Incluso en la estadística descriptiva, los parámetros comunes tienen contrapartes no paramétricas. Aunque los medios y las desviaciones estándar se pueden calcular para cualquier conjunto de números, que son más útiles para resumir los datos cuando los números se distribuyen normalmente. Cuando usted no sabe cómo se distribuyen los números, medianas y cuartiles son mucho más útiles como medidas de tendencia central y de dispersión.




