Cómo utilizar varias funciones de producción de entrada en la economía de la empresa

Funciones de producción múltiple-entrada le permiten dar cuenta de una mayor complejidad en los procesos de toma de decisiones de su empresa. Aunque las funciones de producción de una sola entrada son útiles para ilustrar muchos conceptos, por lo general, son demasiado simplistas para representar decisión de producción de una empresa. En otras palabras, usted está tratando con dos o más insumos variables.

Considere la función de producción q = F(L,K), Que indica la cantidad de salida producida es una función de las cantidades de trabajo, L, y el capital, K, empleada. La forma específica de esta función puede ser la siguiente función Cobb-Douglas

Isocuantas de producción: Todas las combinaciones de entrada son iguales

La relación entre el trabajo, el capital y la cantidad de producción obtenida en la ecuación anterior se describe gráficamente utilizando una isocuanta de producción. LA la producción esoquant muestra todas las combinaciones posibles de dos entradas que producen una cantidad dada de salida.

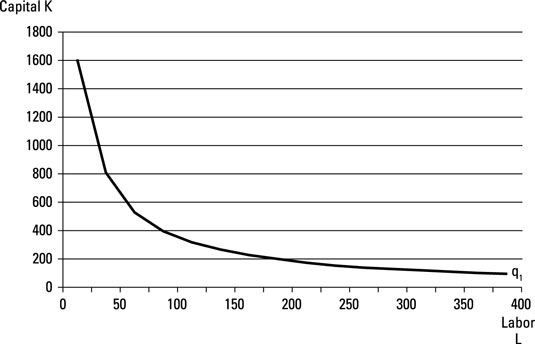
La curva etiquetada q₁ representa todas las combinaciones de capital y trabajo que producen 3.200 unidades de producción.

Producto Marginal

Producto marginal es el cambio en el producto total que se produce da una unidad adicional de una entrada. Con una isocuanta de producción, la cantidad de producción a obtener el uso de una unidad más de trabajo se compensa exactamente por la cantidad de la producción se pierde al usar menos capital.

Cada combinación de entrada de la isocuanta de producción produce el mismo nivel de producción - de salida es constante. El capital puede cambiar por más o menos de una unidad. Lo que es fundamental es que el producto total se mantiene constante a medida que aumenta el trabajo y la reducción de capital.

Tasa marginal de sustitución técnica

los tasa marginal de sustitución técnica mide el cambio en la cantidad de la entrada en el eje vertical del diagrama que es necesario por cambio de una unidad de la entrada en el eje horizontal del diagrama a fin de que el producto total se mantiene constante.

Eso es demasiado técnico de una definición, a fin de recordar este lugar - la tasa marginal de sustitución técnica es simplemente la pendiente de la isocuanta de producción. La pendiente de isocuanta de producción es igual al producto marginal de la entrada en el eje horizontal dividido por el producto marginal de la entrada en el eje vertical.

Curvas isocosto: Todas las combinaciones de entrada cuestan lo mismo

Un factor importante en su decisión de producción es cuánto cuestan las entradas. Si un trabajador adicional (unidad de trabajo) cuesta menos de una unidad adicional de capital, pero el trabajador produce la misma cantidad de producción como capital, que es un buen acuerdo para contratar al trabajador adicional. Por lo tanto, es necesario agregar el costo de su proceso de toma de decisiones.

los curva isocosto ilustra todas las posibles combinaciones de dos entradas que resultan en el mismo nivel de costo total. La curva isocosto se presenta como una ecuación. Para una situación con dos entradas - trabajo y capital - la ecuación de la curva es isocosto

En esta ecuación, C es un nivel constante de costo, p_L es el precio del trabajo, L es la cantidad de trabajo empleado, p_K es el precio del capital, y K es la cantidad de capital invertido.

En un gráfico, la pendiente de la curva de isocosto es igual al precio de la entrada en el eje horizontal dividido por el precio de la entrada de eje vertical.

Suponga que su costo total es de $ 4,000 al día, y la mano de obra cuesta $ 20 por hora, y el capital cuesta $ 5 por máquina horas. Dada esta información, su ecuación de la curva es isocosto

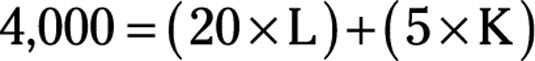
Algunas de las posibles combinaciones de trabajo y capital que puede emplear para un costo total de $ 4000 son 50 horas de trabajo y 600 horas-máquina del capital, de 100 horas de trabajo y 400 horas-máquina del capital, y 150 horas de trabajo y 200 horas de máquina del capital. Cualquier combinación de trabajo y el capital que se traduce en el costo total de ser $ 4000 sería el mismo - $ 4000 - curva isocosto.

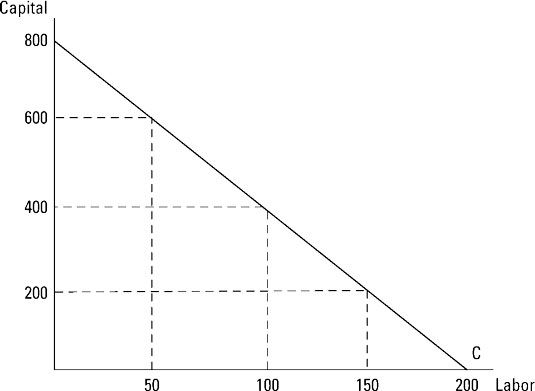
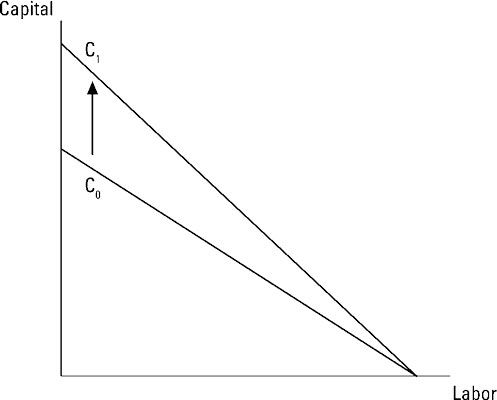
Los cambios en los precios de insumos desplazan la curva isocosto. Si la entrada en el eje horizontal se vuelve más barato, la curva isocosto gira hacia fuera en ese eje. Si la entrada en el eje vertical se vuelve más barato, la curva isocosto gira. Más entradas caros causan cambios en la dirección opuesta.

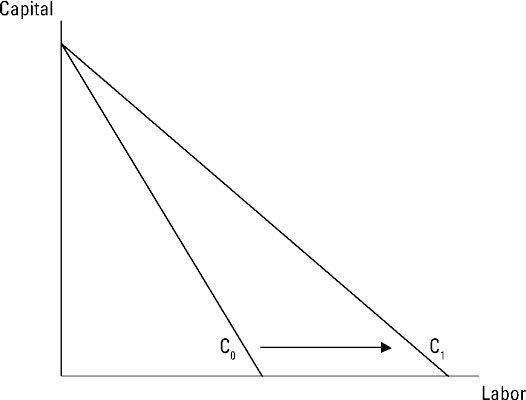
Cómo minimizar los costos

Con el fin de maximizar los beneficios, debe producir su salida al menor costo posible.

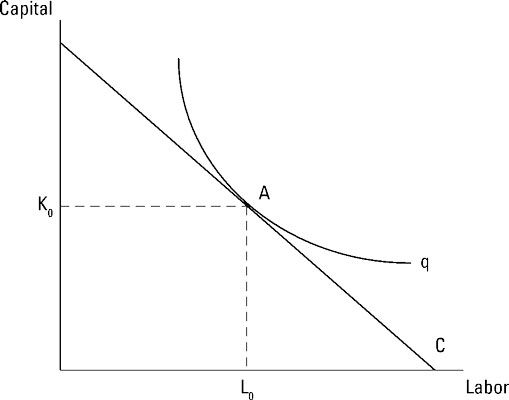
Los costos de producción de una cantidad dada de salida se reducen al mínimo en el punto donde la isocuanta de producción es sólo tangente - o, en otras palabras, sólo tocar - la curva isocosto. Este punto se ilustra como el punto A. La combinación costo minimizar la mano de obra y el capital son las cantidades L₀ y K₀.

Ahora viene la parte fácil. En el punto donde a minimizar los costos, la isocuanta de producción y la curva isocosto son tangentes. Esto significa las laderas de estas dos curvas son iguales. Por Consiguiente

O, si usted reorganizar esa ecuación

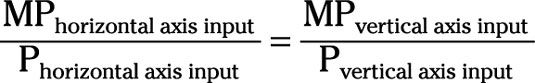
Por lo tanto, a minimizar los costos cuando el producto marginal por dólar gastado en cada entrada es igual para todas las entradas. Y esto es cierto no importa cuántas entradas se utiliza!

Los economistas llaman el concepto anterior a la criterio de menor coste, y es una aplicación de la principio equimarginal. Para producir bienes con el costo de producción más bajo posible, que equipara el producto marginal por dólar gastado.