Cómo calcular la velocidad instantánea con límites

Se puede calcular la velocidad instantánea de un objeto utilizando límites. Digamos que usted y su gato cálculo amante está colgando hacia fuera un día, y usted decide dejar caer una bola fuera de su ventana del segundo piso. Ésta es la fórmula que te dice qué tan lejos la pelota ha caído después de un número determinado de segundos (haciendo caso omiso de la resistencia del aire):

(dónde h es la altura de la pelota ha caído, en pies, y t es la cantidad de tiempo desde que se dejó caer la pelota, en el segundo).

Si enchufa 1 en t, h es de 16 por lo que la bola cae 16 pies durante el primer segundo.

Ahora, lo que si se quería determinar la velocidad de la bola exactamente 1 segundo después de que se te cayó? Puedes empezar por los azotes de esta fórmula de confianza ol:

Usando el tarifa, o velocidad fórmula, puede fácilmente averiguar la velocidad media de la pelota durante el segundo segundo de su caída. Debido a que cayó 16 pies después de 1 segundo y un total de 64 pies después de 2 segundos, cayó 64-16, o 48 pies, desde t = 1 segundo a t = 2 segundos.

La siguiente fórmula le da la velocidad media:

Pero esta no es la respuesta que quiera, porque la pelota se cae cada vez más rápido a medida que cae, y quieres saber su velocidad exactamente 1 segundo después de que se te cae. La pelota se acelera entre 1 y 2 segundos, por lo que este promedio velocidad de 48 pies por segundo durante el segundo segundo es seguro que será más rápida que la bola de instantáneo velocidad al final de su primera segundos.

Para una mejor aproximación, calcular la velocidad media entre t = 1 segundo y t = 1,5 segundos.

Su velocidad media es por lo tanto:

Si continúa este proceso para los tiempos transcurridos de un cuarto de segundo, una décima de segundo, entonces centésimas, milésimas y una diezmilésima de segundo, se llega a la lista de las velocidades medias se muestran en esta tabla.

Como t se acerca más y más cerca de 1 segundo, las velocidades medias parecen estar más cerca y más cerca de 32 pies por segundo.

Esta es la fórmula que se puede utilizar para generar los números de la tabla. Te da la velocidad media entre 1 segundo y t segundos:

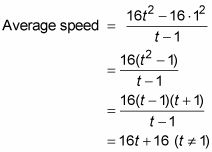
La siguiente figura muestra una gráfica de esta ecuación.

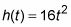
Esta gráfica es idéntica a la gráfica de la línea de y = 16t + 16, excepto para el hoyo en (1, 32).

Hay un agujero, porque si se conecta en 1 t en la función de la velocidad media, se obtiene

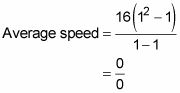
que es indefinido. ¿Y por qué te metiste 0/0? Debido a que usted está tratando de determinar una velocidad media - lo que equivale a distancia total Dividido por tiempo transcurrido - de t = 1 a t = 1. Pero a partir de t = 1 a t = 1 es, por supuesto, no tiempo, y " durante " este punto en el tiempo, la pelota no viaja cualquier distancia, por lo que se obtiene

Obviamente hay un problema aquí. Espera a su sombrero, que has llegado a uno de los grandes " Ah, ja "! momentos en el desarrollo del cálculo diferencial.

Velocidad instantanea se define como el límite de la función de velocidad media como el tiempo transcurrido se aproxima a cero.

El hecho de que el tiempo transcurrido nunca llega a cero no afecta a la precisión de la respuesta a este problema límite - la respuesta es exactamente 32 pies por segundo, la altura del agujero en la figura. Treinta y dos es la respuesta porque como X se acerca más y más cerca de 1, y se acerca más y más cerca de 32. Lo que es notable acerca de los límites es que le permiten calcular la velocidad precisa e instantánea en un solo punto en el tiempo tomando el límite de una función que se basa en una transcurrido tiempo, un período entre de dos puntos de tiempo.