Cómo resolver problemas de ángulo en el PSAT / NMSQT
Cuando dos líneas se encuentran forman un ángulo. Los ángulos se miden en grados. En el PSAT / NMSQT, usted no encontrará ningún ángulos negativos o cero, y probablemente no tendrá que lidiar con los ángulos fraccionarios o bien (sin 45,9 °, por ejemplo). Usted tiene que conocer estos hechos básicos:
Un ángulo recto mide 90 °. Los ángulos rectos son una muy gran cosa, ya que se muestran en una gran cantidad de fórmulas. Si usted ve uno, presta atención.
La suma de los ángulos alrededor de un punto es de 360 °. Piense en las líneas que forman un círculo alrededor de un punto central. Nota: Este hecho aparece en el cuadro de información en el examen.
Un ángulo de la línea recta es igual a 180 °. Cuando dos líneas se encuentran cara a cara, crean un ángulo de la línea recta, que sólo se sienta allí mirando como una línea recta. Si una línea corta a través de una línea recta, los dos ángulos formados son suplementario o suplementario, términos de matemáticas que significan los dos ángulos suman 180 °.
Ángulos opuestos entre sí son iguales. Estos ángulos se llaman también ángulos verticales. En este diagrama, X y y son ángulos verticales.
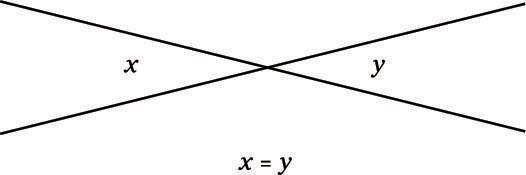
Usted puede ver la frase ángulos verticales en una pregunta de la prueba. No asuma que los ángulos verticales están de pie sólo porque en otros contextos vertical medio en posición vertical. Los ángulos verticales son opuestas entre sí, independientemente de si están arriba y abajo o de lado a lado.
Si una línea corta a través de líneas paralelas, los pequeños ángulos en un solo intersección miden los mismos que los pequeños ángulos en la otra intersección. Del mismo modo, los grandes ángulos en un solo intersección son iguales a los grandes ángulos de intersección en el otro. Echa un vistazo a este esquema:
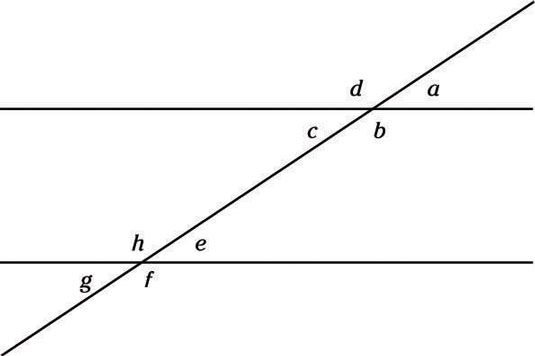
Los pequeños ángulos en la primera intersección son la y c, y los pequeños ángulos en la segunda intersección son e y g. Todos estos ángulos son iguales. Así son los ángulos más grandes: b y d y F y h. Por cierto, ángulos iguales se denominan congruente en matemáticas jerga.
No se le interrogó sobre esta información, pero puede que tenga que utilizarlo en un problema. Echa un vistazo a esta pregunta:
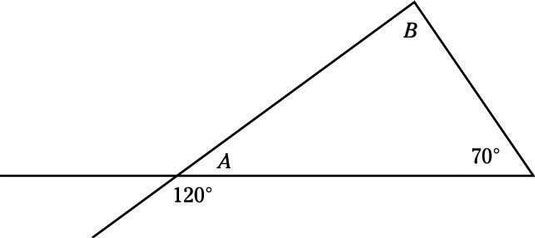
Supongamos que se le pide que encuentre B. Una línea recta es igual a 180 °, para que pueda encontrar LA restando 120 ° de 180 °, lo que le da 60 °. Usted también sabe que los tres ángulos de un triángulo suman 180 °, por lo que 60 ° + 70 ° + B = 180 °. Por Consiguiente, B = 50 °.
Tu turno. Pruebe estos problemas:
En las siguientes figuras, líneas l y m son paralelos. Determinar el valor de X.
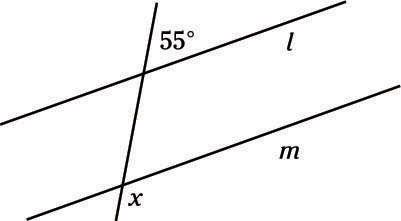
(A) 55 °(B) 75 °(C) 95 °(D) 125 °(E) 155 °
Determinar la medida del ángulo a.
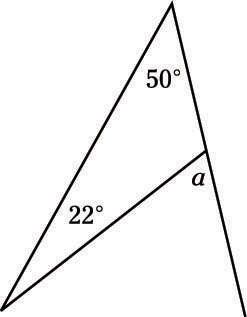
(A) 22 °(B) 33 °(C) 50 °(D) 72 °(E) 108 °
Encuentra el valor de X en la siguiente figura.
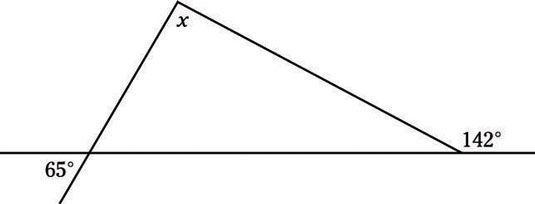
(A) 65 °(B) 77 °(C) 90 °(D) 103 °(E) 142 °
Ahora compruebe sus respuestas.
D. 125 °
Recuerde que las líneas de corte líneas paralelas forman un montón de ángulos iguales. Los ángulos pequeños que las formas cortadas son todos iguales (en este problema, cada uno es 55 °), y todos los grandes ángulos también son iguales (en este problema, que son iguales X).
Se puede ver que el ángulo de 55 ° es complementario a un ángulo grande, por lo que los dos ángulos deben sumar 180 °. Restar: 180 ° - 55 ° = 125 °, por lo que todos los grandes ángulos, incluyendo X, debe medir 125 °, opción (D).
D. 72 °
Usted sabe que hay 180 ° en un triángulo, para que pueda encontrar el tercer ángulo en el triángulo utilizando la resta: 180 ° - 50 ° - 22 ° = 108 °. Ahora que sabes que, se puede ver que 108 ° es suplementaria a la, así la = 180 ° - 108 ° = 72 °, o La opción (D).
B. 77 °
Una vez más, la clave de este problema es saber que hay 180 ° en un triángulo. Usted sabe que el ángulo en la parte inferior izquierda del triángulo mide 65 °, porque es un ángulo vertical con el ángulo marcado 65 °. Usted sabe que el ángulo en la parte inferior derecha del triángulo mide 38 ° porque es complementario del ángulo de 142 ° que está etiquetado.
Encontrar X, sólo hay que restar los números del 180 °: 180 ° - 65 ° - 38 ° = 77 °, opción (B).
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
Interior y ángulos exteriores de un polígono Todo lo que necesita saber acerca de un polígono no necesariamente comprendido en sus lados. Usted puede necesitar para encontrar ángulos exteriores, así como ángulos interiores cuando se trabaja con polígonos:Ángulo interior: Un ángulo…
Proving ángulos verticales son congruentes Cuando dos líneas se cruzan para hacer una X, los ángulos en los lados opuestos de la X se denominan ángulos verticales. Estos ángulos son iguales, y aquí está el teorema oficial que lo dice.Los ángulos verticales son congruentes: Si dos…
Trabajando con más de una transversal Cuando un dibujo de líneas paralelas-with-transversal contiene más de tres líneas, la identificación de ángulos congruentes y complementarias puede ser un poco difícil. La siguiente figura muestra dos líneas paralelas con dos transversales.Si…
Ángulo de elevación y el ángulo de la depresión en las funciones trigonométricas Problemas matemáticos que requieren el uso de funciones trigonométricas a menudo tienen uno de los dos ángulos relacionadas: el ángulo de elevación o el ángulo de depresión. Los escenarios que utilizan estos ángulos por lo general implican…
Cifras trigonométricas básicas Segmentos, rayos y líneas son algunas de las formas básicas que se encuentran en la geometría, y son casi tan importantes en trigonometría. Utiliza esos segmentos, rayos y líneas para formar ángulos.Dibujo segmentos, rayos y líneasLA segmento…
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…
Ángulos gráfico en una posición estándar Navegantes, agrimensores, carpinteros y todos utilizan las mismas medidas de los ángulos, pero los ángulos comienzan en diferentes posiciones o lugares. En trigonometría y la mayoría de las otras disciplinas matemáticas, dibujar ángulos en una…
Cómo cambiar el nombre de los ángulos coterminales Cualquier ángulo puede tener muchas, muchas descripciones en términos de medidas de ángulos, ya que un ángulo es equivalente a sus ángulos coterminales. Las medidas de los ángulos positivos utilizados con mayor frecuencia son los que miden…
Identificar ángulos coterminales Dos ángulos son coterminal si tienen el mismo lado terminal. Usted tiene un número infinito de formas de dar una medida de ángulo de un rayo terminal en particular. A veces, el uso de un ángulo negativo en lugar de un ángulo positivo es más…
Los ángulos positivos y negativos en un círculo unitario El círculo unidad es una plataforma para la descripción de todas las posibles medidas de los ángulos de 0 a 360 grados, todos los negativos de esos ángulos, además de todos los múltiplos de los ángulos positivos y negativos de menos infinito…
Preparación ASVAB: revisión de geometría Usted tendrá que tener un conocimiento básico de la geometría para el ASVAB. Geometry es ". La rama de las matemáticas que se ocupa de la deducción de las propiedades, la medición, y las relaciones de puntos, líneas, ángulos y figuras en el…