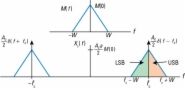
En realidad, varias estaciones de radio operan en la misma área metropolitana, o mercado. Cuando sintonice una señal a 750 kHz, otra señal puede ser a 760 kHz. Para saber si los impactos de señal adyacentes del diseño del receptor simple, asumen que la interferencia es un solo tono, LA_yocos (2# 960-f_yot). La señal recibida es ahora de la forma

con F_yo supone que se encuentran justo fuera del ancho de banda de canal +/- 5 kHz centrada en F_c.

Utilizando una versión generalizada de la fórmula Además fasor, usted puede demostrar que el sobre recibido con la interferencia de un solo tono es el siguiente:

Tenga en cuenta que

El detector de envolvente envolvente recupera R(t). Encontrar R(t) Para un nuevo modelo de señal, utilice la fórmula adicional fasor, que se pueda demostrar que mantener durante amplitudes variables en el tiempo y fases de los términos constituyentes. Los estados fórmula mejorada que

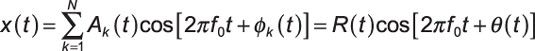
dónde

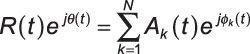
La clave de esta fórmula de trabajo es la común F₀ que se encuentra en cada término coseno.

Para AM más interferencia de un solo tono, se puede hacer el trabajo de fórmula sumando y restando F_c en el término de interferencia:

En la fórmula LA₁(t) = LA_c[1 + soy(t)],

Ahora, calcular

Añadir estos números complejos en forma rectangular y luego encontrar la magnitud:

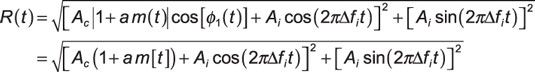
La última línea se sigue de

Porque

usted puede combinar los términos y colocar el valor absoluto. Como comprobación, si LA_yo = 0, es decir, sin la interferencia, el resultado para R(t) Se reduce a

El detector de envolvente es relativamente fácil de implementar en hardware, pero es un poco difícil de analizar. Usted puede explorar el modelo de R(t) Para tener una idea de lo que está pasando. Para empezar, la relación de entrada / salida no es lineal, como se evidencia por las plazas y las operaciones de raíz cuadrada. Incluso con LA_yo = 0, R(t) Contiene un valor absoluto. En este punto, asumir m(t) = Cos (2# 960-f_mt) De casos de prueba tan simple.

La función de Python env_plot (t, Ac, AM, FM, Ai, fi) permite R(t) Para ser trazado, así como su espectro. El espectro P_R(F) Es un resultado del uso de PyLab psd () función.

En [346]: Def env_plot (t, Ac, AM, FM, Ai, fi): ...: R = sqrt ((Ac + Am * cos (2 * pi * fm * t) + Ai * cos (2 * pi * dfi * t)) ** 2 + (Ai * sin (2 * pi * t * DFI)) ** 2) ..: volver REn [347]: T = arange (0,20,1 / 500.) # T = 20 ms, fs = 500 kHz

Ejercer la función mediante el uso de un vector de tiempo de funcionamiento de más de 20 ms a una frecuencia de muestreo efectiva de 500 KSPS y luego trazar el dominio del tiempo y dominio de la frecuencia resultados de lado a lado (véase la matriz subtrama 3 x 2 en la figura).

Set

Ajuste también LA_m = 0,5, que es equivalente a establecer la = 0,5 (50 por ciento profundidad de modulación). El valor de LA_yo pasos más de 0, 0,1, y 1,0. El mensaje de 2 kHz está dentro del requisito de ancho de banda mensaje 5-kHz y

kHz para la interferencia coloca en el canal adyacente (5 kHz es la frecuencia de cruce).

Aquí están las entradas principales de la línea de comandos IPython:

En [447]: R = env_plot (t, 1, .5,2,0,7) En [449]: Plot (t, r) En [454]: Psd (R, 2 ** 13500) -En [457]: R = env_plot (t, 1, .5,2,0.1,7) En [459]: Plot (t, r) En [464]: Psd (R, 2 ** 13500) -En [467]: R = env_plot (t, 1, .5,2,1,7) En [469]: Plot (t, r) En [475]: Psd (R, 2 ** 13500) -

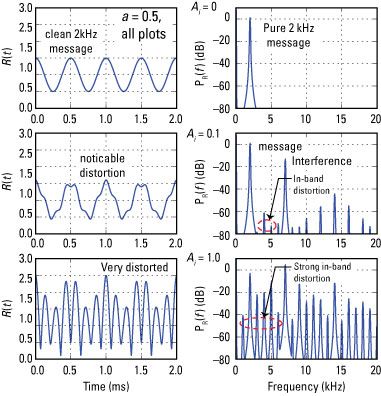
La única manera de eliminar o reducir la interferencia es con un BPF en frente del detector de envolvente. La opción superheterodino es una buena opción aquí, debido a que el BPF no necesita ser sintonizable. Al principio, puede que moleste que una señal fuera de banda puede producir interferencias en banda, pero siempre se debe esperar lo inesperado de la no linealidad. La ventaja es que el diseño del receptor sigue siendo bajo costo.

Diagrama de bloques

2

Adyacente canales Interferencia

3

AM Radio Diseño

4