Matemáticas normas fundamentales comunes: estadística y probabilidad

Estadísticas

(que analiza los datos existentes) y probabilidad (que utiliza los datos existentes para predecir acontecimientos futuros) son dos ramas de las matemáticas necesarias para Estándares Básicos Comunes que los estudiantes pueden ver en el trabajo en el mundo.

Las estadísticas se utilizan en todo, desde medir cómo los ciudadanos se sienten acerca de un determinado político para fijar las primas de seguros para informar el debate sobre el cambio climático. La probabilidad se utiliza a menudo para tomar decisiones, como cuándo plantar un cultivo determinado, ya sea una empresa debe expandirse, o si un individuo debe postularse para un cargo político.

Cómo interpretar los datos categóricos y cuantitativos

Expectativas en esta llamada zona en que los estudiantes se reúnen, analizan y presentan dos tipos de datos:

• Categórico: Los datos categóricos se utiliza a menudo para comparar y contrastar grupos- por ejemplo, un estudio muestra que el coche color más popular es blanco. La plata y negro están empatados en el segundo.

• Cuantitativo: Los datos cuantitativos representa mediciones, como la longitud, el número de votos, la densidad de población, y así sucesivamente.

Los estudiantes muestran datos en varias formas, incluyendo líneas de números, gráficos y tablas que utilizan diversas medidas del centro y métodos para determinar los patrones, la repetición, y las tendencias en los datos. Algunos términos comunes que es probable encontrar son

• significar (la media)

• mediana (el número medio cuando los datos se organizan de menor a mayor)

• desviacion estandar (una descripción de la distancia desde el centro en una colección de datos)

• correlación (cuando la frecuencia o la ocurrencia de dos cosas están relacionadas)

• causalidad (cuando algo provoca otro evento suceda)

He aquí un ejemplo de un problema típico que requiere el uso de los datos existentes para hacer predicciones sobre situaciones futuras: Imagine que un banco es más ocupado 16:00-18:00 en las noches entre semana. Durante estas horas, el tiempo de espera en el drive-through normalmente distribuido, con una media de 8 minutos y una desviación estándar de 2 minutos.

El uso de las desviaciones estándar, determinar: a) el porcentaje de clientes que esperar 10 minutos o más, b) el porcentaje que esperar entre 4 y 12 minutos, y c) el porcentaje que esperar 2 minutos o menos.

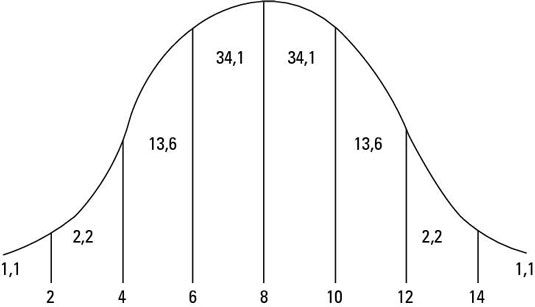
Dibuja una curva de campana estándar y luego hacer los cálculos:

1. 10 minutos o más:

   Añadir los porcentajes en el 10-12, 12-14 y> 14 rangos: 13,6 + 2,2 + 0,1 = 15,9 por ciento

2. 4 a 12 minutos:

   Añadir los porcentajes en los 4-6, 6-8, 8-10 y 10-12 rangos: + 34,1 + 13,6 34,1 + 13,6 = 47,7 + 47,7 = 95,4 por ciento

3. A menos de 2 minutos:

   Tome el porcentaje en el lt; 2 rango: 0,1 por ciento

   

Hacer inferencias y justificar conclusiones

Los estudiantes descubren las estadísticas como una manera de averiguar acerca de una población o grupo sin reunir necesariamente la información de cada persona en esa población. Esto incluye la toma de inferencias - conclusiones basadas en la evidencia. Al mirar los métodos para hacer determinaciones sobre las poblaciones de eventos utilizando los métodos estadísticos, los estudiantes discuten si los métodos son fiables - por ejemplo, si las personas encuestadas son realmente representativos de toda la población.

Los estudiantes también exploran los usos de aleatorización para mejorar la exactitud de los datos. Por ejemplo, en ensayos clínicos de nuevos medicamentos, los participantes en el estudio son casi siempre elegidos al azar para los dos grupos - el grupo que recibe el medicamento y el otro grupo que recibe el placebo, por ejemplo. Este enfoque disminuye la posibilidad de que algún otro factor se sesgar los resultados.

Por ejemplo, si un grupo consistía exclusivamente en los hombres y la otra de las mujeres, los resultados podrían ser influenciada por el sexo de los participantes en lugar de por si la medicación fue más eficaz que el placebo.

Con su hijo, examinar una encuesta reciente llevada a cabo en un asunto político. Discuta todos los componentes utilizados en la recogida de datos, tales como el tamaño de la población de la muestra, los medios de recopilación de datos y la interpretación de los resultados. Comparte tus opiniones sobre la fiabilidad de las conclusiones extraídas de los datos.

Identificar casos en los que la aleatorización de la recogida de datos es apropiado para la validez estadística y para eliminar el potencial de sesgo (en otras palabras, para garantizar que los datos no está inclinada en cualquier dirección particular).

Reglas de probabilidad condicional y probabilidad

Matemáticas de alta escuela incluye el estudio de la probabilidad condicional - es decir, la probabilidad de que el resultado de un evento influirá en el resultado de otro evento. Los estudiantes exploran técnicas para determinar si dos sucesos son independiente (ni evento influye en el otro evento) o condicional (la probabilidad de un evento que ocurre está influenciada por si se produce otro evento).

Los estudiantes también descubren cómo utilizar los datos para predecir la probabilidad de ciertos eventos cuando múltiples opciones están involucrados. La probabilidad de eventos compuestos (cuando el mismo ensayo se intenta varias veces con las mismas circunstancias) también se trata en estos estándares.

Esto es un problema de ejemplo: Usted dibuja al azar dos cartas de una baraja de 52 cartas. ¿Cuáles son las probabilidades de dibujo dos clubes?

Una baraja de cartas tiene 13 clubes, lo que significa que tiene un 13 en 52 o 1 en 4 posibilidades de elaboración de un club como la primera tarjeta. Para el segundo sorteo, sólo 12 clubes siguen siendo de 51 cartas en total. Esto se traduce en un 4 sobre 17 la posibilidad de que le sacas un club en el segundo sorteo.

Para determinar la probabilidad de que esto ocurra en sorteos consecutivos, multiplicar las dos relaciones:

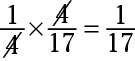
Usted tiene un 1 en 17 probabilidades de dibujo dos clubes consecutivamente.

Utilice la probabilidad para tomar decisiones

Una de las razones más convincentes para desarrollar una habilidad para el cálculo de probabilidades es porque esta habilidad a menudo le permite tomar mejores decisiones. Los estudiantes usan la probabilidad para evaluar la probabilidad de que el número de ocurrencias o eventos dentro de un conjunto de datos y luego utilizar esa información para responder a preguntas o sacar conclusiones basadas en los resultados.

Los estudiantes también hacen uso de la probabilidad para determinar el resultado de eventos basados ​​en el azar y analizar la toma de decisiones en ciertos escenarios.