Cómo crear e interpretar caja y bigote parcelas para un proyecto seis sigma

Como poner a dos personas de regreso a la vuelta para ver quién es más alto, Sigma Seis usos caja y bigote parcelas (o solo diagramas de caja) la comparación directa de dos o más distribuciones de variación. Cuando usted necesita para comparar las distribuciones de valor para múltiples características, pocas cosas son más rápidas para hacer o fáciles de interpretar que una caja y bigotes.

Una caja y bigotes parcela se compone de una caja, que representa la masa central de la variación, y las líneas finas, llamado bigotes, que se extienden a ambos lados y representan las colas de adelgazamiento de la distribución.

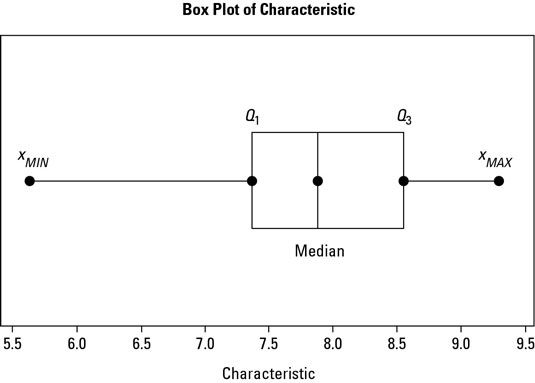
Para crear un cuadro y la trama de la barba, sólo tienes que seguir estos pasos:

1. Clasifique las mediciones de datos en orden de menor a mayor.

2. Determinar la mediana de los datos.

   Encontrar el valor observado en los datos de rango ordenado donde la mitad de los datos se encuentra por encima y la otra mitad se encuentra a continuación.

3. Cuando el número de puntos observados (n) En el conjunto de datos es impar, tomar

   

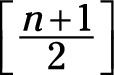
   Ese valor en la secuencia jerarquizada es su medio. Por ejemplo, si n es igual a 99, tome 99 + 1 = 100 y luego dividir ese resultado por 2 para obtener 50. El número 50 en su lista es la mediana.

4. Cuando n es par, la mediana es la media de la

   

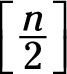
   y el

   

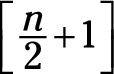
   valores en la secuencia jerarquizada. Si n = 100, que iba a encontrar 100 247- # 2 y (100 # 247- 2) + 1. Esas expresiones que dan 50 y 51, por lo que iba a encontrar la 50ª y 51ª valores y el promedio de ellos para encontrar la mediana.

5. Encuentra el primer cuartil, Q1.

   los primer cuartil marca el punto 25 por ciento en sus específicos de secuencia de tres cuartas partes de rango ordenado de los datos están aún por venir.

6. Encuentra el tercer cuartil, Q3.

   los tercer cuartil Se queda el punto 75 por ciento en su rango por orden de secuencia de una cuarta parte de los datos.

7. Encontrar el mayor valor observado, X_MAX, y el valor observado más pequeño, X_MIN.

8. Dibuja una línea horizontal, que representa la escala de medida de la característica.

   Esta escala puede ser en milímetros de longitud, libras de peso, minuto para el tiempo, el número de defectos encontrados en una parte inspeccionado, o cualquier otra cosa que cuantifica qué aspecto de la característica que le interesa.

9. Marque su mediana y cuartiles valores de los pasos 2 a 4 y la construcción de la caja.

   Hacer puntos para sus mediana y cuartiles valores. Dibuje un cuadro que abarca desde el primer cuartil (Q₁) Para el tercer cuartil (Q₃) Y trazar una línea vertical en el cuadro correspondiente al valor de la mediana.

10. Añadir los valores máximo y mínimo de la Etapa 5 y construir los bigotes.

    Dibuja dos líneas horizontales, que se extiende hacia fuera de la Q₁ valor a la observación más pequeña observada, X_MIN, y otro que se extiende hacia fuera de la Q₃ valor al mayor valor observado, X_MAX.

11. Repita los pasos 1 a 8 para cada característica adicional que se trazó y se compara con la misma escala horizontal.

Cuando usted tiene un gran conjunto de datos para una característica, es posible que desee ampliar las barbas a cabo sólo a los percentiles 10 y 90, o para los percentiles 5 y 95 y así sucesivamente, en lugar de los valores máximo y mínimo. Luego, cuando los puntos de datos atípicos caen más allá de estos extremos de los bigotes, puede dibujarlos como puntos inconexos o estrellas.

Este método es una gran manera de gráfica identificar y comunicar la presencia de valores atípicos en los datos.

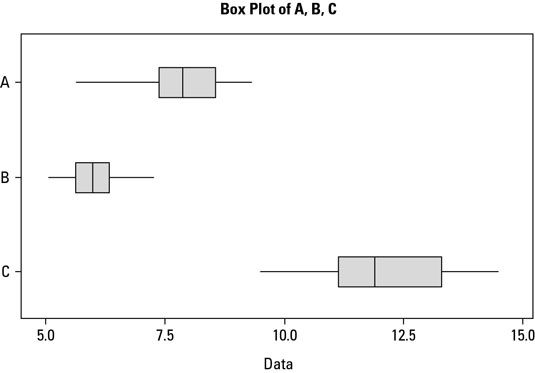
Caja y bigotes parcelas son ideales para comparar dos o más distribuciones de variación, como antes y después de puntos de vista de un proceso o formas características o alternativos de llevar a cabo una operación. En esencia, cuando se quiere averiguar rápidamente si dos o más distribuciones de variación son diferentes (o el mismo), se crea un diagrama de caja.

Distribución B tiene claramente el nivel más bajo. Sin embargo, todavía se solapa con el rendimiento de la distribución LA, lo que indica que puede que no sea tan diferentes. Distribución C, Por otro lado, tiene un valor mucho mayor y ninguna superposición con las distribuciones LA y B. También tiene un margen mucho más amplio para su variación.

Otras cosas que debe buscar en gráficos de caja comparativos son las siguientes:

• Las diferencias o similitudes en lugar de la mediana

• Las diferencias o similitudes en anchos de caja

• Las diferencias o similitudes repartidas bigote a bigote

• Se superponen o brechas entre distribuciones

• Variación sesgada o asimétrica en las distribuciones

• La presencia de valores atípicos