Los estadísticos robustos y grandes datos
Una estadística se dice que es robusto si no está fuertemente influenciada por la presencia de valores atípicos. Por ejemplo, la media no es robusta, ya que puede estar fuertemente afectada por la presencia de valores atípicos. Por otro lado, la mediana es robusto - no se ve afectada por los valores extremos.
Por ejemplo, supongamos que los siguientes datos representa una muestra de los ingresos familiares en un pequeño pueblo (medido en miles de dólares al año):
32, 47, 20, 25, 56
A calcular la media de la muestra como la suma de las cinco observaciones dividido por cinco:
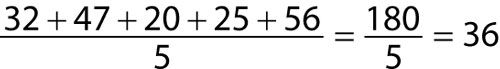
La media de la muestra es de $ 36,000 por año. La mayoría de los hogares de la muestra están muy cerca de este valor.
Supongamos que en vez de que la muestra se compone de los siguientes valores:
32, 47, 20, 25, 376
Debido a que el ingreso familiar de $ 376.000 es sustancialmente mayor que el ingreso familiar más próximo de $ 32.000, el ingreso familiar de $ 376.000 puede ser considerado como un caso atípico.
Con el valor atípico, la muestra quiere decir que hoy es la siguiente:
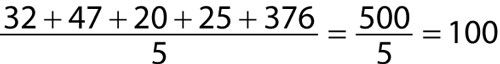
Esta medida no es representativa de la mayoría de los hogares de la ciudad. Por lo tanto, la utilidad de la media se ve comprometida en la presencia de valores atípicos.
Usted calcular la mediana de la muestra por la clasificación de los datos de menor a mayor y luego encontrar el valor que divide la muestra en medio. En otras palabras, la mitad de las observaciones están por debajo de la mediana, y la otra mitad por encima.
La primera muestra:
32, 47, 20, 25, 56
La muestra ordenados:
20, 25, 32, 47, 56
En este caso, la mediana es 32 porque la mitad de las observaciones restantes están por debajo de 32 y la otra mitad por encima de ella.
La segunda muestra:
32, 47, 20, 25, 376
La muestra ordenados:
20, 25, 32, 47, 376
A pesar de la presencia del atípico de 376, la mediana es todavía 32. No se ha visto afectada por el valor atípico. Esto demuestra que a diferencia de la media, la mediana es robusto con respecto a los valores atípicos.
Otros ejemplos de estadísticas sólidas incluyen la mediana, desviación absoluta, y el rango intercuartil.
-
Encuentra los valores atípicos en los datos de infografía -
Los diagramas de caja: técnica gráfica de datos estadísticos -
Análisis exploratorio de datos gráfica (eda) técnicas -
Pruebas gráficas de los valores extremos de datos -
Pruebas de hipótesis para los valores extremos de datos -
Diagramas de tallo y hojas: técnica gráfica de datos estadísticos
Tendencia central: allá de lo básico La media y la mediana son las dos medidas más fiables y comúnmente reportados del centro, y se utilizan en una amplia variedad de situaciones. Sin embargo, si usted está estudiando seriamente estadísticas, usted debe estar familiarizado con las…
Comparando los histogramas En la interpretación de los gráficos en las estadísticas, puede que te encuentres tener que comparar dos o más gráficos. Los siguientes histogramas representan las calificaciones en un examen final común a partir de dos secciones diferentes de…
Los conjuntos de datos y problemas de estadística descriptiva Sea consciente de las unidades de cualquier estadística descriptiva a calcular (por ejemplo, dólares, pies o millas por galón). Algunas estadísticas descriptivas están en las mismas unidades que los datos, y algunos no lo son. Resuelve los…
Cómo la forma de un histograma refleja la media y la mediana estadística Puede conectar la forma de un histograma con la media y la mediana de los datos estadísticos que se utilizan para crearlo. Por el contrario, la relación entre la media y la mediana puede ayudar a predecir la forma del histograma.El gráfico…
¿Cómo encontrar el rango intercuartil para una muestra estadística Para obtener una medida de la variación sobre la base del resumen de cinco números de una muestra estadística, usted puede encontrar lo que se llama la rango intercuartil, o IQR.El propósito del resumen de cinco números es dar la estadística…
¿Cómo encontrar el valor de la mediana de un conjunto de datos estadísticos La mediana es una estadística que se utiliza comúnmente para medir el centro de un conjunto de datos. Sin embargo, todavía es un héroe anónimo de las estadísticas en el sentido de que no se utiliza con tanta frecuencia como debe ser, aunque la…
Cómo identificar skew y la simetría en un histograma estadística A veces la media debate entre medio puede llegar a ser muy interesante. Especialmente cuando se mira a la asimetría y la simetría de sus datos estadísticos en un histograma.Por ejemplo, supongamos que usted es parte de un equipo de la NBA…
Cómo localizar un valor en un conjunto de datos utilizando cuartiles Cuartiles dividir un conjunto de datos en cuatro partes iguales, cada uno compuesto de 25 por ciento de los valores ordenados en el conjunto de datos. Cuartiles están relacionados con percentiles, así:En primer cuartil (Q1) = Percentil 25En…
¿Cómo hacer un diagrama de caja de un resumen de cinco números LA diagrama de caja es un gráfico unidimensional de datos numéricos basados en el resumen de cinco números. Este resumen incluye las siguientes estadísticas: el valor mínimo, el percentil 25 (conocido como Q1), La mediana, el percentil 75…
Medidas de tendencia central Medidas de tendencia central muestran el centro de un conjunto de datos. Tres de las medidas más utilizadas de tendencia central son la media, la mediana y la moda.SignificarSignificar es otra palabra para la media. Esta es la fórmula para el…
Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…
Estadísticas para grandes datos para los maniquíes Medidas de tendencia central muestran el centro de un conjunto de datos. Tres de las medidas más utilizadas de tendencia central son la media, la mediana y la moda.SignificarSignificar es otra palabra para la media. Esta es la fórmula para el…