Cómo la forma de un histograma refleja la media y la mediana estadística

Puede conectar la forma de un histograma con la media y la mediana de los datos estadísticos que se utilizan para crearlo. Por el contrario, la relación entre la media y la mediana puede ayudar a predecir la forma del histograma.

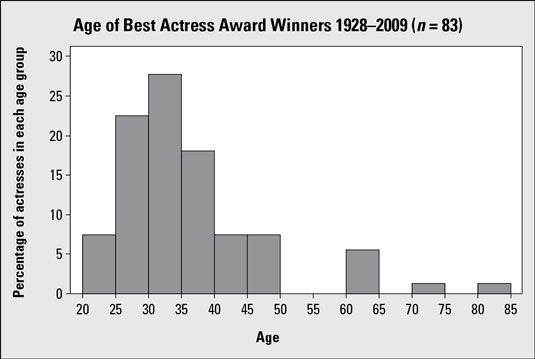
El gráfico anterior es un histograma que muestra las edades de ganadores de la Academia a la Mejor Actriz Award-se puede ver que es sesgada a la derecha. La siguiente tabla incluye cálculos de algunos básicos (es decir, descriptivos) estadísticas del conjunto de datos. El examen de estos números, se encuentra la media de edad es de 33.00 años y la edad media es 35,69 años:

La edad media es superior a la media de edad a causa de unas pocas actrices que eran un poco más viejo que el resto cuando ganaron sus premios. Por ejemplo, Jessica Tandy ganó por su papel en Paseando a Miss Daisy cuando tenía 81, y Katharine Hepburn ganó el Oscar a la En el estanque dorado cuando tenía 74. La relación entre la mediana y la media confirma la asimetría (a la derecha) que se encuentra en el primer gráfico.

Estos son algunos consejos para la conexión de la forma de un histograma con la media y la mediana:

• Si el histograma está sesgada a la derecha, la media es mayor que la mediana.

  Este es el caso porque los datos asimétricos derecho tienen unos valores grandes que impulsan la media hacia arriba, pero no afectan en el que el centro exacto de los datos es (es decir, la mediana).

• Si el histograma está cerca de simétrica, entonces la media y la mediana son cerca uno del otro.

  Cerca simétrica significa que los datos son más o menos la misma en altura y ubicación en cada lado del centro de la histogram- no necesita ser exacta.

  Cerca se define en el contexto de la de datos, por ejemplo, los números 50 y 55 se dice que son cerca si todos los valores se encuentran entre 0 y 1000, pero se considera que son más separados si todos los valores se encuentran entre 49 y 56.

  El histograma se muestra en este gráfico está cerca simétrica. Su media y la mediana son ambos iguales a 3,5:

  

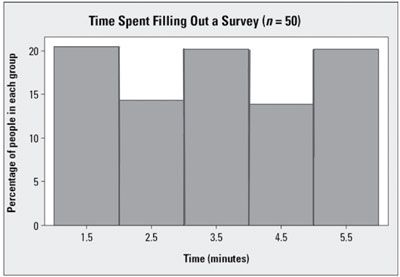
• Si el histograma es sesgada a la izquierda, la media es menor que la mediana.

  Este es el caso porque los datos-sesgada a la izquierda tienen unos valores pequeños que impulsan la media hacia abajo, pero no afectan en el que el centro exacto de los datos es (es decir, la mediana).

  El siguiente gráfico representa los resultados del examen de 17 estudiantes, y los datos son asimétricos izquierda. La media y la mediana del conjunto de datos original se calculan para ser 70.41 y 74.00, respectivamente. La media es inferior a la media debido a un par de estudiantes que obtuvieron un poco más bajo que los otros. Estos hallazgos coinciden con la forma general del histograma se muestra en el gráfico:

  

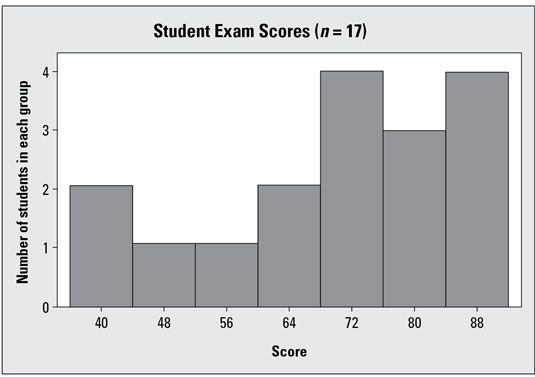
Si por alguna razón usted no tiene un histograma de los datos, y sólo tiene la media y la mediana de ir cerca, puedes compararlas entre sí para obtener una idea aproximada en cuanto a la forma del conjunto de datos.

• Si la media es mucho mayor que la mediana, los datos son generalmente sesgada a la derecha; unos pocos valores son más grandes que el resto.

• Si la media es mucho menor que la mediana, los datos son generalmente sesgada a la izquierda; unos valores más pequeños traen la media hacia abajo.

• Si la media y la mediana están cerca, usted sabe los datos es bastante equilibrada, o simétrica, en cada lado (aunque no necesariamente en forma de campana).