Otros "medios" (además de la media aritmética) para medir la tendencia central

Varios otros tipos de medios, además de la aritmética, son medidas útiles de tendencia central en ciertas circunstancias. Se llaman medio

porque todos ellos implican el mismo "sumarlos y dividir por la cantidad de" proceso como la media aritmética, sino que cada uno presenta un giro ligeramente diferente al proceso básico.

Media Interior

los medio interno (también llamado el Media Truncada) De N números se calcula mediante la eliminación de el valor más bajo y el valor más alto y el cálculo de la media aritmética de los restantes N - 2 valores "internos". Para el ejemplo IQ (84, 84, 89, 91, 110, 114 y 116), que le deje caer uno de los valores más bajos (un 84) y el valor más alto (116), y calcular la media interior como (84 + + 91 + 89 110 + 114) / 5 = 488/5 = 97,6.

Una media incluso "interno-er" se puede calcular por la caída de los dos (o más) más altos y dos (o más) valores más bajos de los datos y calculando la media aritmética de los valores restantes. En aras de la equidad, siempre se debe picar el mismo número de valores de la gama baja a partir de la gama alta.

Al igual que la mediana, la media interior es más resistente a los valores extremos que la media aritmética. Y, si se piensa en ello, si usted cortar un número suficiente de ambos extremos del conjunto ordenado de los valores, que finalmente le dejó con sólo el medio de uno o dos valores - este "centro de la est" promedio en realidad sería la mediana!

Significado geometrico

los significado geometrico (GM a menudo abreviado) puede ser definido por dos fórmulas de aspecto diferente que producen exactamente el mismo valor. La definición básica tiene esta fórmula:

Esta fórmula le está diciendo que multiplicar los valores de la N observaciones juntos (eso es lo que # 928-, el símbolo "capital Pi", indica), y luego tomar la N^º raíz del producto. El ejemplo IQ (84, 84, 89, 91, 110, 114 y 116) se ve así:

Esta fórmula puede ser difícil de evaluate incluso computadoras pueden tener problemas con el gran producto que podría ser generada en el cálculo del GM de una gran cantidad de números. Mediante el uso de logaritmos (que a su vez multiplicaciones en sumas y raíces en divisiones), se obtiene una fórmula alternativa "numéricamente estable":

Esta fórmula puede parecer complicado, pero en realidad sólo dice: "La media geométrica es la antilog de El aritmética significar de El registros de los números. "Usted toma el registro de cada número, medios todos los registros de la forma habitual, y luego tomar el antilogaritmo de la media. Puede utilizar logarithms- natural o común sólo asegúrese de usar el mismo tipo de antilogaritmo.

La media geométrica se utiliza a menudo al resumir datos asimétricos, especialmente si hay razones para creer que los datos podrían ser distribuidos logarítmica normal, debido a que los logaritmos de los valores de una distribución logarítmica normal se distribuyen normalmente.

Media cuadrática

los media cuadrática (RMS) de un montón de números se define de esta manera:

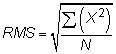
Usted cuadrados cada número, medios todos esos cuadrados de la forma habitual, y luego tomar la raíz cuadrada de la media. Por ejemplo, el RMS de los dos números 10 y 20 es

El RMS es útil para resumir el tamaño de las fluctuaciones aleatorias. De hecho, la desviación estándar de un conjunto de números se calcula mediante un método que es casi idéntico al cálculo de los RMS de las desviaciones de cada valor de la media de esos valores.