Variación directa e inversa en el PSAT / NMSQT

No todos los problemas de álgebra en el PSAT / NMSQT es una ecuación. Puede que tenga que averiguar lo que le sucede a uno la cantidad cuando se varía directamente o inversamente en relación con otra cantidad. Sin sudar. Usted ya sabe cómo resolver estos problemas.

Preguntas variación directa son relaciones sólo disfrazados. Para resolver un problema en el que dos cantidades (digamos, la y b) Varían directamente, recuerde que la relación de la a b es una constante. (¿Qué constante? Eso es probablemente lo que la pregunta que usted quiere saber.) Establecer una relación con los valores originales de la y b marcado con el subíndice 1 y los nuevos valores marcados con un 2:

Ahora se puede cruzar-multiplicar y resolver. Aquí está la razón para esta pregunta: En la fiesta de Adán, el número de globos inflados (12) varió directamente con el número de globos reventados antes de la fiesta, incluso comenzó (8). ¿Cuántos globos se abrirá antes del próximo partido de Adán si infla 36 globos?

Está bien, llamar a los globos inflados la₁ y los globos estallar b₁. Así la₁ es 12 y b₁ es 8. Su relación es entonces

Cuando cruzada multiplica, se obtiene288 = 12b₂

Ahora divide cada lado de la ecuación por 12, y se obtiene 24 = b₂. Su respuesta es de 24, globos-basura listo desinflados.

Observe que cuando una variable aumenta, la otra variable también lo hace. Usted puede eliminar algunas opciones rápidamente si usted recuerda este hecho acerca de la variación directa.

Ya por variación inversa. Aquí, el producto de las dos variables (por ejemplo, la y b) Es siempre el mismo número, o constante. Así que si a = 7 y b = 9, la constante es 7 x 9 o 63. Así que si la es 3, b debe ser de 21 años, debido a 3 x 21 = 63.

Si el número de globos destruido por la rasgadura o pinchar antes de la fiesta varía inversamente, Adam puede perder 7 a rasgaduras y 9 a los pinchazos, o 3 a rasgaduras y 21 a los pinchazos. De cualquier manera que su partido va a faltar en la decoración.

Prueba estas preguntas de práctica:

1. El número de problemas de palabras de un profesor de matemáticas asigna varía directamente con el número de preguntas que se le pide durante la clase. Ella asignó 6 problemas de palabras el lunes después se les pidió 15 preguntas. Si se les pidió 20 preguntas el miércoles, ¿cuántos problemas palabra qué se asigna?

   (A) 4(B) 6(C) 8(D) 10(E) 15

2. Los valores de p y q variar de forma inversa. Cuando p tiene un valor de 8, q tiene un valor de 10. ¿Cuál es el valor de p cuando q es 4?

   (A) 2(B) 5(C) 10(D) 20(E) 40

Ahora compruebe sus respuestas:

1. C. 8

   Recuerde, variación directa significa que la relación es constante, por lo que estableció una ecuación:

   

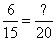
   Puede cruzada multiplican resolver o ver que la primera fracción se reduce a 2.5, lo que significa que por cada 5 preguntas, el profesor asigna 2 problemas de palabras. Esto significa que cuando el profesor escucha 20 preguntas (4 x 5), que va a asignar 4 x 2 = 8 problemas de palabras, Choice (C).

2. D. 20

   Cuando estás tratando con variables que varían inversamente, recuerde siempre que la multiplicación es la clave. No importa que p y q están, siempre deben multiplicarse en el mismo valor. Los valores dados, 8 y 10, se multiplican a 80, por lo que todo p-q pares deben multiplicarse hasta 80. Cuando q es 4, p debe ser (80/4) = 20, Choice (D).