Cómo ace problemas de relación en el PSAT / NMSQT
En las secciones de matemáticas PSAT / NMSQT, puede encontrar preguntas sobre relaciones. Los porcentajes son todos acerca de la relación entre una parte y el todo. Ratios expresar la relación entre partes.
Se oye referencias a las relaciones de todo el tiempo cuando la gente dice cosas como, " la temporada pasada que el lanzador entregado siete ponches por cada nueve paseos, " o, " la proporción de guisantes a las zanahorias en el cuadro promedio es de ocho a uno ". Tenga en cuenta que en estos comentarios que no son dado el número total de bateadores lanzador enfrentó o la cantidad de verduras picadas en marcha que puede tener para la cena.
Una vez más, las relaciones son acerca partes, no totalidades.
Ratios se escriben normalmente con un colon (un punto encima de otro), de esta manera:
La relación entre sorbos de eructos es 12: 5.
Cuando se lee la frase en voz alta, los dos puntos se convierte en " a, " como en, " la relación entre sorbos de eructos es de 12 a 5. "
En el PSAT / NMSQT, se le puede pedir sobre posible totales. La suma de las partes es un total posible, pero también lo son todos los múltiplos de esa suma. Así que si la proporción de mayores de biología de Grandes Ligas francesas es de 4 a 3, el número total de carreras francés y biología puede ser 7, 14, 21, 28. . . usted consigue la idea!
Si se le pregunta a decir lo es o debe ser del total, la respuesta es no puede ser determinado, porque cualquier múltiplo de 7 es posible, en base a la suma de las partes de relación.
Backsolving ayuda con ratios. Si se le pregunta sobre un total posible, busque una opción de respuesta que es un múltiplo de la suma de las partes.
A veces, los responsables de las pruebas que dan al total y la relación y le piden que averiguar cuántos hay en cada parte, como en esta pregunta:
George engulle 2 caramelos de goma para cada 3 gusanos de goma. Si George tiene 75 piezas de dulces, ¿cuántos granos de la jalea tiene?
George tendrá un dolor de estómago grave, pero no te preocupes para usted, porque usted sólo tiene que seguir estos pasos:
Añadir las partes.
Usted sabe dulce alijo de George contiene caramelos de goma y gusanos de goma en una proporción de 2: 3 y 2 + 3 = 5.
Divida el total de por la suma que ha calculado.
De acuerdo, 75 dividido por 5 le da una cociente (lo que se obtiene cuando se divide), de 15.
Multiplique cada parte de la relación en el cociente.
Así que tienes 2 x 15, lo que equivale a 30 caramelos de goma, y 3 x 15, lo que equivale a 45 gusanos de goma.
Revise su trabajo mediante la adición de las partes.
Su total debe ser 75 y 30 + 45 lo hace de hecho la igualdad 75.
Engullir un gomoso-lo que sea y dar vuelta a su atención a estas cuestiones.
La relación de los niños a los adultos en una sala de cine es de 2: 5. Si el teatro tiene 175 personas, ¿cuántos de ellos son niños?
(A) 2(B) 50(C) 100(D) 125(E) 150
Una bolsa contiene canicas y dados. Si la relación de canicas a los dados en la bolsa es de 4: 5, lo que es un número total posible de mármoles y dados en la bolsa?
(A) 27(B) 28(C) 29(D) 30(E) 31
Equipo de ajedrez de Chester Middle School tiene una serie de perder proporción de 9: 4. Si el equipo ganó 99 de los juegos de ajedrez que jugaron, ¿cuántos juegos jugaron en total?
(A) 140(B) 141(C) 142(D) 143(E) 144
Ahora compruebe sus respuestas:
B. 50
Si la relación de los niños con los adultos es de 2: 5, a continuación, los niños constituyen la siguiente parte de la audiencia.
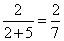
Ahora sólo tienes que multiplicar la proporción de niños por el número total de personas:
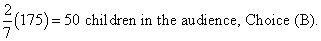
A. 27
Usted sabe que por cada 4 canicas hay 5 dados, por lo que su número total de canicas y dados debe ser un múltiplo de 4 + 5 = 9. La opción (A) es el único que es un múltiplo de 9, por lo que es el que está buscando!
D. 143
Para llegar desde la relación de ganar al número ganador de los juegos, sólo tiene que multiplicar por 11 (porque 99 = 9 x 11), por lo que el número de partidos perdidos también debe ser la relación de partidos perdidos multiplica por 11 o 44 juegos . Añadir juntos 99 ganadores y 44 derrotas, y usted tiene un total de 143 partidas de ajedrez. Jaque mate con Choice (D)!
-
Cálculo de una distribución por ciento en excel -
Conecte ratios y fracciones en matemática núcleo común -
Resolver problemas de tasas y de relación en matemáticas núcleo común -
¿Cómo aplicar la tabla de la alegría a las preguntas de relación -
¿Cómo trabajar con razones y proporciones -
Razones y proporciones
Saber trabajar con relaciones en las pruebas de aritmética Una razón es por lo general un par de números con dos puntos entre ellos, tales como 2: 1. Describe el tamano relativo de dos cosas - si te imaginas a dos personas separando un montón de dulces (o billetes de igual valorada, o cualquier otra…
Preparación núcleo Praxis: cómo calcular la probabilidad Para la Praxis Core, que se centrará en la probabilidad de un evento, también conocido como P (evento), que se ocupa de cómo algo tan probable es que se produzca. Puede grabar la probabilidad de un evento como una fracción, decimal o…
Estrategias de Ley para la resolución de razones y proporciones Algunas de las preguntas de matemáticas en la ACT implicarán razones y proporciones. Ambos problemas de razón y proporción entrañan la comparación de cantidades, y requieren que usted sabe cómo trabajar con fracciones y la forma de resolver…
Variación directa e inversa en el PSAT / NMSQT No todos los problemas de álgebra en el PSAT / NMSQT es una ecuación. Puede que tenga que averiguar lo que le sucede a uno la cantidad cuando se varía directamente o inversamente en relación con otra cantidad. Sin sudar. Usted ya sabe cómo…
Sáb prueba de muestra de matemáticas: Las preguntas de la calculadora En la sección calculadora de la nueva prueba SAT Matemáticas, se obtiene 55 minutos para hacer frente a 37 preguntas. Las 30 preguntas de opción múltiple tienen ahora cuatro respuestas a elegir en vez de cinco. Seis preguntas de matemáticas…
Cómo resolver problemas de círculo en el PSAT / NMSQT Círculos están por todas partes, sobre todo en el PSAT / NMSQT. No es casualidad que el Inglés contiene muchas referencias a los círculos: círculo de amigos, el agua dando vueltas el desagüe, que viene completo círculo, etcetera. Al llegar a…
Definiciones importantes en las secciones de matemáticas / NMSQT PSAT La aritmética que aprendió en la escuela primaria y secundaria que sirve bien cuando estás trabajando en números y operaciones preguntas sobre el PSAT / NMSQT. Sin embargo, cuando se resuelve un problema en el PSAT / NMSQT, es posible que…
Ratios financieros clave para la alta potencia de inversión Las razones financieras, o ratios contables, ofrecen a los inversores una forma de analizar la información con el fin de evaluar la salud financiera de una empresa. Los valores utilizados en el cálculo de las proporciones vienen de contables o…
Relaciones actuales y rápidas Si el pasivo corriente se vuelven demasiado altos en relación con los activos actuales - que constituyen la primera línea de defensa para el pago de pasivos actuales - los gerentes deben actuar con rapidez para resolver el problema. La escasez…
¿Cómo las empresas a determinar el patrimonio a activos totales Algunas compañías están particularmente interesados en la proporción de sus activos totales que se compone de participación en el capital, porque esta relación puede disminuir la cantidad que tienen que pedir prestado para generar la…
¿Cómo leer los estados financieros con relaciones En vez de realmente leer su camino a través de los estados financieros - es decir, la digestión cuidadosamente cada línea reportado en todos los estados financieros - es uno de los enfoques para calcular ciertas razones para extraer los mensajes…
Cómo utilizar los informes financieros para el cálculo de la relación deuda-capital Los prestamistas están siempre asegúrese de buscar en la deuda en los informes financieros utilizando el relación deuda-capital, que mide el apalancamiento de una empresa al ver qué porción de su capital proviene de financiación de la…