Definiciones importantes en las secciones de matemáticas / NMSQT PSAT

La aritmética que aprendió en la escuela primaria y secundaria que sirve bien cuando estás trabajando en números y operaciones preguntas sobre el PSAT / NMSQT. Sin embargo, cuando se resuelve un problema en el PSAT / NMSQT, es posible que encuentre algo así como una de estas frases:

Tres primo números añadidos a. . .La mayor positivo número es . . .LA entero negativo multiplicada por . . .

No se puede hacer el problema si usted no sabe qué tipo de números que está tratando. Afortunadamente, la prueba de los responsables por lo general se limitan a algunos términos clave.

• Un entero puede ser o bien positivo (mayor que cero) o negativo (menor que cero). Cero es también un entero, pero es ni positivo ni negativo- que está en una clase por sí mismo. Los enteros nunca son decimales o fracciones.

• LA número entero es un número positivo que nunca incluye fracciones o decimales. Los números enteros son incluso (divisible por 2) o impar (no divisible por 2). Cero es también un número entero.

• LA numero primo sólo tiene dos factores- no puede ser dividido por otra cosa que no sea en sí y 1. (En caso de que usted se esté preguntando, 1 y 0 son no números primos.)

• LA factor de un número es cualquier número que divide perfectamente en otra, más grande, el número sin dejar un residuo. Por ejemplo, 3 es un factor de 21, ya que cuando se divide 21 por 3, se obtiene 7 y ningún resto.

• Una palabra más esencial vocabulario es consecutivo (siguiendo una tras otra, sin interrupción, como en “, 8, 9, 10 ").

Cuando se lee una pregunta números y operaciones, adquirir el hábito de subrayar el tipo de número que está buscando. Mantener el tipo de número en su mente a medida que trabaja a través del problema y seleccionar una respuesta.

Echa un vistazo a estos ejemplos de preguntas.

1. El producto de tres números impares consecutivos es 315. ¿Cuál es el más pequeño de estos enteros?

   (A) 3(B) 5(C) 7(D) 9(E) 11

2. Tres números primos se multiplican entre sí. ¿Cuál de las siguientes afirmaciones, en su caso, debe ser verdad?

   I. El producto debe ser impar.II.El producto debe ser primordial.III.El producto debe tener exactamente 5 factores.(A) Yo sóloSolamente (B) IISolamente (C) III(D) I y III(E) ninguna de las anteriores

3. ¿Cuál es la suma de los números enteros en el conjunto

   

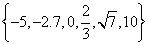
   (A) -7,7(B) -5(C) 3,3(D) 5(E) 10

Ahora compruebe sus respuestas:

1. B. 5

   Enchufar es una gran manera de resolver este problema. Recuerde, usted quiere probar Choice (C) primero. Si 7 es el número más pequeño, a continuación, 9 y 11 son los otros dos números. Multiplique los tres juntos y se obtiene 693 - demasiado grande. Trate Choice (B): 5 x 7 x 9 = 315, y que ha encontrado su respuesta!

   Subrayando los términos clave de la cuestión es una gran manera de enfocar su atención en los detalles importantes. En la pregunta 1, es posible destacar " consecutivo, " " impar, " " más pequeño, " y " # 148 enteros.;

2. E. ninguna de las anteriores

   ¿Qué tan bien conoces a tus números primos? Recuerde que 2 es la única aun número primo, así que si usted multiplica 2 por otros dos números primos, el resultado es par. Por lo tanto, la opción no es necesariamente cierto. Si estás multiplicar tres números juntos para obtener su producto, entonces cada uno de esos números es un factor del producto, por lo que el producto no puede haber mejor momento. Por lo tanto, la opción II está fuera.

   Y Opción III es un truco! Elija tres números primos a ver qué pasa: 2, 3, y 5 funcionará, y su producto es de 30. Usted sabe que 2, 3, y 5 son todos los factores, pero también lo es el producto de dos de ellas: 6, 10 y 15. Además, recuerde que el 30 y 1 son factores. Su respuesta es opción (E).

3. D. 5

   Usted sabe que los números enteros son números enteros positivos o negativos, o 0. Los enteros en el conjunto son -5, 0 y 10. Cuando se agregan juntos, la suma es 5, opción (D).