Estrategias de Ley para la resolución de razones y proporciones
Algunas de las preguntas de matemáticas en la ACT implicarán razones y proporciones. Ambos problemas de razón y proporción entrañan la comparación de cantidades, y requieren que usted sabe cómo trabajar con fracciones y la forma de resolver mediante el uso de álgebra.
Una razón es una comparación de dos cantidades sobre la base de la operación de división. Por ejemplo, si una escuela tiene un profesor por cada ocho estudiantes, se puede expresar la relación de maestro a estudiante en cualquiera de las siguientes maneras:
Observe que este ratio expresa la proporción de profesores a los estudiantes. Así, el 1 va delante de la 8 y, en la fracción, el 1 va en la parte superior de la 8.
Al contestar una pregunta de ACT que incluye una relación, una buena estrategia es la de expresar la relación como una fracción equivalente. A continuación, puede sacar todas las herramientas que ya tiene para trabajar con fracciones - por ejemplo, la reducción, la conversión a decimales, y así sucesivamente.
Ejemplo 1
Una empresa tiene un total de 150 empleados, 25 de los cuales son administradores. ¿Cuál es la relación de los administradores a los no administradores?
(A) 1-3
(B) 1 a 4
(C) 1-5
(D) de 1 a 6
(E) de 2 a 5
La empresa cuenta con 25 directivos, por lo que los 125 empleados restantes no eran administradores. Expresar esta relación como una fracción y luego reducirlo:
La relación de los directivos a los no gerentes es de 1 a 5, por lo que la respuesta correcta es la opción (C).
Una de las aplicaciones más prácticas de la proporción es una proporción, que es una ecuación basada en una relación. Por ejemplo, si usted sabe la proporción de niños a las niñas, se puede expresar esto como una fracción, configurarlo igual a otra fracción que incluye una variable, y luego resolver. El siguiente ejemplo ilustra cómo funciona este concepto.
Ejemplo 2
Un campamento de verano tiene una relación de niño a niña de 08:11. Si el campo tiene 88 niños, lo que es el número total de niños en el campamento?
(F) 121
(G) 128
(H) 152
(J) 176
(K) 209
Comience por la creación de la proporción en la siguiente ecuación:
Antes de continuar, se dio cuenta de que la relación menciona específicamente chicos y chicas primeros segundos, por lo que este se mantenga el orden en la ecuación. El campamento cuenta con 88 chicos, por lo que sustituye a este número para Niños en la ecuación. No sabes cuántas niñas hay, por lo que utiliza la variable g. Esto es lo que la ecuación ahora queda como:
Para saber cuántas niñas se encuentran en el campamento, resolver g utilizando el álgebra. En primer lugar, cruzada multiplicar para deshacerse de las dos fracciones:
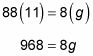
Ahora divide ambos lados por 8:
121 = g
El campamento cuenta con 121 niñas y 88 niños, por lo que sé que tiene un total de 209 niños-, por lo tanto, la respuesta correcta es Choice (K).
-
Conecte ratios y fracciones en matemática núcleo común -
Resolver problemas de tasas y de relación en matemáticas núcleo común -
La proporción áurea -
¿Cómo aplicar la tabla de la alegría a las preguntas de relación -
Cómo convertir entre fracciones y decimales que se repiten -
¿Cómo aumentar los términos de una fracción
¿Cómo trabajar con razones y proporciones LA proporción es una comparación matemática de dos números, basado en la división. Por ejemplo, supongamos que traer 3 camisas y 5 lazos con usted en un viaje de negocios. Aquí hay algunas maneras de expresar la relación de las camisas de los…
En fracciones, uno es el número más fácil Con fracciones, la relación entre los números, no los números reales en sí, es más importante. Comprender cómo multiplicar y dividir fracciones pueden darle una comprensión más profunda de por qué se puede aumentar o disminuir los números…
Dar sentido a porcentajes La palabra por ciento literalmente significa "el 100", pero en la práctica, significa más cerca de "fuera de 100." Por ejemplo, supongamos que una escuela tiene exactamente 100 niños - 50 niñas y 50 niños. Se puede decir que "50 de 100" niños…
Razones y proporciones LA proporción es una comparación matemática de dos números, basado en la división. Por ejemplo, supongamos que traer 2 bufandas y 3 tapones con usted en unas vacaciones de esquí. Aquí hay algunas maneras de expresar la relación de pañuelos…
¿Cómo trabajar ambos lados de una identidad trig Con una identidad trigonometría, trabajando en ambos lados de la ecuación es aún más divertido que trabajar en ambos lados de una algebraico ecuación. En álgebra, puede multiplicar cada lado por el mismo número, cuadrado ambos lados, añadir…
El intervalo de confianza en torno a una proporción Si se va a encuestar a 100 niños típicos y encontrar que 70 de ellos como el chocolate, que le estimar que el 70 por ciento de los niños como el chocolate. ¿Cuál es el intervalo de confianza del 95 por ciento (CI) en torno a que la estimación…
¿Cómo trabajar con fracciones molalidad y topo Al igual que la diferencia en sus nombres, la diferencia práctica entre molaridad y molalidad es sutil. Echa un vistazo de cerca a sus definiciones, expresadas uno junto al otro en las siguientes ecuaciones:Los numeradores en cálculos molaridad y…
Preguntas de práctica pre-álgebra en el acto En el examen de matemáticas ACT, alrededor de un # 8208-cuarto de las preguntas cubre pre-álgebra (personas normales se refieren a esto como la aritmética). Estas preguntas pueden incluir conceptos tales como fracciones, decimales y restar…
ASVAB aritmética subprueba razonamiento: que muestran comparaciones con relaciones Usted tendrá que saber cómo trabajar con las proporciones de la subprueba de razonamiento aritmético del ASVAB. LA proporción muestra una relación entre dos cosas. Por ejemplo, si Margaret invirtió en su salón de tatuajes en una relación 2:…
Preparación ASVAB: trabajar con fracciones Cuando vas a tomar el ASVAB, usted debe saber cómo trabajar con fracciones. Habrá varias preguntas de prueba de su capacidad y experiencia en esta región matemática.La realización de varias operacionesA veces hay que hacer más de una…
Resolver problemas de proporcionalidad directa en el acto El ACT probablemente incluirá algunos problemas de matemáticas que involucran proporcionalidad directa. P DirectoPROPORCIONALIDAD se refiere a una relación entre dos variables en base a cualquiera de multiplicación o división, donde las…
Variación directa e inversa en el PSAT / NMSQT No todos los problemas de álgebra en el PSAT / NMSQT es una ecuación. Puede que tenga que averiguar lo que le sucede a uno la cantidad cuando se varía directamente o inversamente en relación con otra cantidad. Sin sudar. Usted ya sabe cómo…