La proporción áurea
Razones y proporciones son una parte importante del estudio de las matemáticas, la ciencia y los negocios. Una relación puede escribirse como una fracción, y una proporción es una declaración que dos razones son iguales. Las propiedades de las proporciones son más útiles en la resolución de problemas cuyas ecuaciones utilizar proporciones.
En primer lugar, tenga en cuenta las propiedades de las proporciones. Teniendo en cuenta la proporción
lo siguiente es cierto:
Los productos cruzados son iguales: una d = bc.
Los recíprocos son iguales:
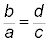
Las siguientes fracciones se pueden reducir como de costumbre.
Las fracciones en la siguiente pueden reducirse verticalmente u horizontalmente mediante la eliminación de los factores comunes:
Así que, si la = ef y c = por ejemplo,, después
Y si b = jk y d = jm, después
Estas propiedades se utilizan para trabajar con el proporción áurea, la relación encontrada en el rectángulo áureo. El rectángulo áureo se cree que es la forma más agradable estéticamente y aparece en obras maestras como la Mona Lisa y en otro arte y la arquitectura de los siglos.
En Euclides's Elementos, a encontrar una de las definiciones primera escritas de esta proporción áurea: " se dice una línea recta para haber sido cortada en extrema y media razón cuando, como toda la línea es al segmento mayor, por lo que es la mayor a la menor ". ¿Qué, es que el griego para usted?
Considere un segmento dividido en dos partes, la y b, que representa la proporción áurea.
El segmento la es 1 unidad de largo, y el segmento la + b es de aproximadamente 1.618 unidades de largo, una aproximación de la proporción áurea. Por lo tanto, la proporción
El símbolo aproximada se utiliza aquí porque la proporción áurea es un número irracional y tiene un decimal que nunca termina o se repite. ¿Qué tiene de especial esta relación particular?
Volver a la definición de Euclides, la " como a toda la línea es al segmento mayor " (la longitud es 1,618 a 1) " por lo que es la mayor a la menor " (la longitud es 1 a 0.618). El radio
La proporcion
Para encontrar el valor exacto de la proporción áurea, considere la proporción
Si la longitud de la es 1 unidad, entonces la proporción se convierte
Utilice la propiedad cruzada de productos para obtener (1 + b)b = 1 o b + b2 = 1. En la forma estándar de una ecuación de segundo grado en b, Tienes b2 + b - 1 = 0. Para resolver b, que necesita la fórmula cuadrática:
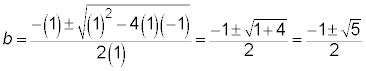
Se tiene en cuenta únicamente la suma en el numerador, porque
es un número negativo y no puede representar la longitud del segmento. Entonces deja
Ahora calcular la + b mediante la sustitución de la la con 1 y la b con la solución de la fórmula cuadrática, y usted tiene:
El valor de
o la proporción áurea.
Razones y proporciones LA proporción es una comparación matemática de dos números, basado en la división. Por ejemplo, supongamos que traer 2 bufandas y 3 tapones con usted en unas vacaciones de esquí. Aquí hay algunas maneras de expresar la relación de pañuelos…
Cómo resolver problemas de triángulos similares con el teorema de lado divisor Usted puede resolver ciertos problemas de triángulos similares utilizando el Side-divisor teorema. Este teorema afirma que si una línea es paralela a un lado de un triángulo y que interseca los otros dos lados, se divide esos lados…
Cómo utilizar el teorema del ángulo bisectriz El teorema de ángulo-Bisectriz establece que si un rayo biseca un ángulo de un triángulo, a continuación, se divide el lado opuesto en segmentos que son proporcionales a los otros dos lados. La siguiente figura ilustra esto.El teorema de ángulo…
Cómo utilizar la proporción áurea La proporción áurea es una famosa idea de la geometría con una conexión a la antigua Grecia. (Cuando se trataba de matemáticas, física, astronomía, filosofía, teatro, y similares, los antiguos griegos Seguro hice patear algunos traseros…
Cómo comparar dos proporciones poblacionales A efectos estadísticos, se puede comparar dos poblaciones o grupos cuando la variable es categórica (por ejemplo, fumador / no fumador, Demócrata / Republicano, el apoyo / oposición de una opinión, etc.) y que está interesado en la proporción…
¿Cómo encontrar probabilidades para una proporción de la muestra Usted puede encontrar las probabilidades de una proporción de la muestra mediante el uso de la aproximación normal, siempre y cuando se cumplan ciertas condiciones. Por ejemplo, digamos que un estudio estadístico afirma que 0,38 o 38% de todos…
¿Cómo encontrar la distribución de muestreo de una proporción de la muestra Si utiliza un tamaño suficiente gran muestra estadística, se puede aplicar el teorema del límite central (CLT) a una proporción de la muestra para los datos categóricos para encontrar su distribución muestral. los proporción de la población,…
Cómo cambiar radianes a grados Se utiliza la misma proporción básica para cambiar radianes a grados como lo hace para cambiar grados a radianes. El cálculo requerido para el cambio de radianes a grados no es difícil. Por ejemplo, para cambiarradianes a una medida en…
La función coseno: adyacente sobre la hipotenusa La función trigonométrica coseno, abreviado cos, funciona mediante la formación de esta relación: adyacente / hipotenusa. En la figura, se ve que los cosenos de los dos ángulos son los siguientes:La situación con las proporciones es el mismo…
El intervalo de confianza en torno a una proporción Si se va a encuestar a 100 niños típicos y encontrar que 70 de ellos como el chocolate, que le estimar que el 70 por ciento de los niños como el chocolate. ¿Cuál es el intervalo de confianza del 95 por ciento (CI) en torno a que la estimación…
Estrategias de Ley para la resolución de razones y proporciones Algunas de las preguntas de matemáticas en la ACT implicarán razones y proporciones. Ambos problemas de razón y proporción entrañan la comparación de cantidades, y requieren que usted sabe cómo trabajar con fracciones y la forma de resolver…
Niveles de Fibonacci y el comercio de tendencia Después de desarrollar su teoría de la onda de Elliott, Ralph Nelson Elliott observó que los patrones de ondas se relacionan con la Secuencia fibonacci. los Secuencia fibonacci es una serie de números creados mediante la adición de la suma de…