Resolver problemas de tasas y de relación en matemáticas núcleo común
Alumnos de sexto grado a resolver una variedad de problemas matemáticos básicos comunes utilizando ratios. Las palabras proporción y tarifa son a la vez apropiado en sexto grado y en su mayoría se pueden utilizar indistintamente.
LA proporción es una comparación de dos números del mismo tipo (unidad). Por lo general, la relación se utiliza para la parte # 8208-parte comparaciones, pero no siempre. La palabra tarifa hace que la mayoría de la gente piensa en el cambio, pero una tasa es una comparación de dos números de diferentes tipos (o unidades). La mayoría de la gente usa el término proporción en situaciones en que los números no cambian y el uso tarifa cuando los números están cambiando.
Ejemplos de tarifas, los estudiantes trabajan con incluyen
Dólares por hora
Millas por hora
Dólares por libra
Estudiantes por clase
Alumnos de sexto grado a desarrollar una variedad de estrategias para resolver problemas de relación y de tipos. Por ejemplo, considere este problema:
La proporción de niños a las niñas en la clase de la Sra Gales es 3: 2. Si hay 30 estudiantes en la clase, ¿cuántos son niños y cuántas son niñas?
Los estudiantes pueden resolver este problema con un tabla de razones, como se muestra en la figura.
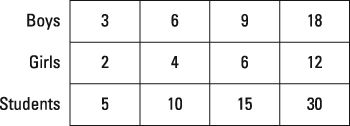
En una tabla de razones, un estudiante hace un seguimiento de diferentes formas equivalentes de la relación. El estudiante puede doble (o triple, etc.) cada valor de la relación para obtener valores más grandes o puede reducir a la mitad (o cortar en tres, y así sucesivamente) cada valor para obtener valores más pequeños. No hay dos tablas de relación para el mismo problema tienen que parecer idénticos, pero sí necesitan para mantener la relación dada en todas partes.
Un estudiante puede notar que si hay 3 niños por cada 2 chicas, a continuación,
de los estudiantes son chicos. Ella puede escribir la siguiente serie de fracciones con el fin de averiguar el número correcto de los niños para una clase de 30 estudiantes. En este caso, cada fracción representa la parte de la clase que son los chicos:
La última fracción muestra que 18 de los 30 estudiantes son muchachos en este escenario.
Lo importante de relaciones es que son de multiplicación comparaciones # 8208 con sede en de dos números. Si ambos números dobles en una relación - por ejemplo 3: 2 se convierte en 6: 4 - la relación de multiplicación entre el número sigue siendo el mismo. En este ejemplo, 6 es aún
veces más grande que 4, al igual que 3 es
tan grande como 2.
-
¿Cómo funciona la herencia en c ++? -
Sumar y multiplicar fracciones en matemática núcleo común - Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 1
- Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 5
- Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 6
- Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 7
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 8 En 8º grado, los estudiantes se sienten más cómodos con el uso de los números racionales e irracionales para cumplir con las normas fundamentales comunes. LA número racional es uno que puede ser expresado como una fracción simple. Un numero…
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 3 La multiplicación, división y fracciones son componentes clave de las habilidades y conceptos estudiantes encuentran a las normas fundamentales comunes en el grado 3. Los estudiantes también continúan trabajando con las formas. Estándares…
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 4 Después de aprender los conceptos básicos de la multiplicación, la división y fracciones en el Grado 3, Grado 4 estudiantes ponen sus habilidades para trabajar por la aplicación de estos conceptos fundamentales comunes a la multi-paso problemas…
Comparar fracciones en una recta numérica en matemáticas núcleo común En Common Core matemáticas, estudiantes de tercer grado usan una línea de números para ver cómo fracciones se relacionan entre sí. Una línea número es útil para mostrar la ubicación relativa de las fracciones, así como su distancia uno de…
Conecte ratios y fracciones en matemática núcleo común En Common Core matemáticas, los estudiantes de sexto grado estudian proporciones y las fracciones que se establecen en contextos comprensibles, y ellos trabajan con el fin de formular y responder preguntas interesantes y desafiantes.LA proporción…
¿Cómo los niños se comparan los números en matemáticas núcleo común En Common Core matemáticas, muchas preguntas importantes requieren la comparación de los números para decidir qué número es mayor, o si los números son iguales. Un estudiante de kindergarten que pueden contar hasta 20 todavía puede tener que…
Cómo factores y múltiplos están relacionados de matemáticas básico común En cuarto grado de matemáticas, los estudiantes Common Core comienzan a estudiar cómo los números se construyen a partir de las relaciones de multiplicación. La relación importante aquí es entre los factores y múltiplos.Un número de factores…
Matemáticas normas fundamentales comunes: el sistema de los números reales Los estudiantes de secundaria deben tener un entendimiento del sistema de números reales para satisfacer las normas fundamentales comunes. los sistema de números reales contiene todos los números que se pueden representar en una recta numérica,…
Multiplique con unidades, pares, y las matrices de matemáticas básico común En Common Core matemáticas, los estudiantes de tercer y cuarto grado comienzan a estudiar la multiplicación. La fundación para la multiplicación es igual # grupos 8.208 empresas, ya sean unidades, pares, o matrices.Para prepararse para este…
Resuelve proporciones en matemáticas núcleo común Ser capaz de resolver proporciones es importante en séptimo grado de matemáticas. En un aula básico común, el énfasis está en dar sentido al método de solución, más que en la memorización de un procedimiento dado.Una regla general para si…
Resolver problemas de variables y equivalencia en matemáticas núcleo común Sexto grado es la primera vez que los estudiantes de matemáticas básicos comunes empiezan a resolver problemas utilizando variables y la propiedad de la equivalencia (en concreto, la propiedad distributiva).Se suelen utilizar las variables que…
¿Cómo trabajar con razones y proporciones LA proporción es una comparación matemática de dos números, basado en la división. Por ejemplo, supongamos que traer 3 camisas y 5 lazos con usted en un viaje de negocios. Aquí hay algunas maneras de expresar la relación de las camisas de los…