Resolver problemas de proporcionalidad inversa en el acto
El ACT probablemente incluirá algunos problemas de matemáticas que involucran proporcionalidad inversa. P Inversa
PROPORCIONALIDAD se refiere a una relación entre dos variables en base a cualquiera de multiplicación o división, donde las variables tienden a subir y bajar por separado. Es decir, como una aumenta, la otra disminuye, y viceversa.Dos variables, X y y, son inversamente proporcionales cuando la siguiente ecuación se cumple para alguna constante k:
xy = k
Proporcionalidad inversa significa que a medida que el valor de una variable cambia, el otro valor también debe cambiar de modo que cualquier producto resultante xy permanece constante.
Ejemplo 1
Dos variables p y q son inversamente proporcionales, de tal manera que si p = 4, entonces q = 8. ¿Cuál es el valor de q cuando p = 16?
(A) 1
(B) 2
(C) 4
(D) 16
(E) 32
El producto pq es una constante y
Por lo tanto, pq = 32 para todos los posibles emparejamientos de p y q. Sustituto de 16 de p en esta ecuación:
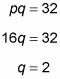
Por lo tanto, la respuesta correcta es la opción (B).
Ejemplo 2
Si
y uv = 10, ¿cuál de los siguientes debe ser verdad?
(F)t y u son inversamente proporcionales
(G)t y v son inversamente proporcionales
(H)t y w son directamente proporcionales
(J)t y w son inversamente proporcionales
(K)u y v son directamente proporcionales
Comience cruzada multiplicador:
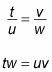
Sustituto de 10 de uv:
tw = 10
Por lo tanto, tw = k para k = 10, por lo t y w son inversamente proporcionales. Así que la respuesta correcta es la opción (J).
-
Cómo declarar variables en C ++ -
Cómo asignar valores a las variables en su ti-84 Calculator Plus -
Matemáticas normas fundamentales comunes: álgebra -
Cómo hacer generalizaciones en la econometría con valor esperado o media -
En la econometría, la función inversa limita el valor de la variable dependiente -
Cómo utilizar las funciones para describir las relaciones económicas
¿Cómo resolver ecuaciones lineales con dos multiplicación y división A menudo, es necesario utilizar tanto la multiplicación y la división para resolver una ecuación lineal. Cuando una ecuación lineal utiliza tanto la multiplicación y la división, a resolver mediante la operación inversa de cada uno. Por lo…
Sistemas de ecuaciones de álgebra Resolver En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una…
¿Cómo resolver un sistema de ecuaciones utilizando la inversa de una matriz Si usted tiene un coeficiente ligado a una variable en un lado de una ecuación matricial, se puede multiplicar por inversa del coeficiente de hacer ese coeficiente desaparece y te deja con sólo la variable. Por ejemplo, si 3X = 12, ¿cómo…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
Cómo utilizar CCTA después de probar triángulos semejantes CCTA es simplemente un acrónimo que significa "ángulos correspondientes de triángulos semejantes son congruentes. ' A menudo se utiliza CCTA en una prueba inmediatamente después de probar triángulos semejantes (exactamente de la misma manera…
Determinar el papel de las variables en psicología estadística En psicología estadística, estudios de investigación que impliquen la recolección datos cuantitativos (todos los datos que se puede contar o representa como números) por lo general requieren que usted pueda recoger y almacenar datos en una hoja…
Cómo aceleración centrípeta mantiene un objeto que se mueve en un círculo constante En física, cuando un objeto se desplaza en movimiento circular uniforme, su velocidad es constante, lo que significa que la magnitud de la velocidad del objeto no cambia. Por lo tanto, la aceleración no puede tener ningún componente en la misma…
Preparación núcleo Praxis: cómo trabajar con funciones Las funciones se presentan generalmente en forma de ecuaciones en la Praxis Core. Una función puede tener un aspecto de miedo con la F(X) Anotación al inicio de la ecuación, pero no tienes nada de qué preocuparse. Si usted puede resolver…
Pre-álgebra y fórmulas de álgebra que usted debe saber para el acto Algunas de las preguntas sobre el acuerdo examen ACT de matemáticas con problemas pre-álgebra y álgebra. Sólo hay unas pocas fórmulas para recordar, pero son vitales.Aquí hay dos importantes fórmulas pre-álgebra que usted necesita…
Resolución de problemas de palabras acto utilizando un sistema de ecuaciones Resolución de problemas de palabras es una de las razones más comunes de utilizar un sistema de ecuaciones. Por ejemplo, algunos problemas de palabras en el examen ACT de matemáticas que sería difícil acercarse utilizando una única variable es…
Resolver problemas de proporcionalidad directa en el acto El ACT probablemente incluirá algunos problemas de matemáticas que involucran proporcionalidad directa. P DirectoPROPORCIONALIDAD se refiere a una relación entre dos variables en base a cualquiera de multiplicación o división, donde las…
Estrategias para resolver sistemas de ecuaciones en el acto LA sistema de ecuaciones es un conjunto de dos o más ecuaciones que incluyen dos o más variables. Para resolver un sistema de ecuaciones en el examen ACT de matemáticas, necesita una ecuación para cada variable en el sistema. Esto generalmente…