Preguntas de función en el PSAT / NMSQT

Usted encontrará algunas preguntas de función de la parte de matemáticas del PSAT / NMSQT. Funciones son como las computadoras. Usted algo de entrada, X, y algo más sale. La variable, X, puede cambiar. (Es por eso que se llama una variable!) Cada vez X cambios, también lo hace el resultado. Usted puede expresar funciones en diferentes maneras. Se empieza con un largo y elegante f. Entonces usted tiene algo entre paréntesis, por lo general X.

Esta expresión dice lo eff del ex. Algunas funciones parecen ecuaciones:

F(X) = -3X + 8

La diferencia entre esta función y otra ecuación es que se puede conectar cualquier cosa en el punto variable y terminar con otra respuesta correcta. En otras palabras, los números en funciones vienen en pares. Las funciones también pueden ser escritos como gráficos. Aquí hay una tabla de algunos valores de la función anterior:

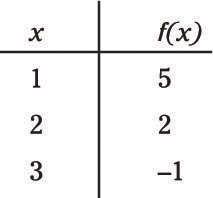
Una función también puede aparecer como un gráfico. He aquí una gráfica de la función anterior:

Para el PSAT / NMSQT, es necesario conocer de cerca y personal con lineal y quadratic funciones. Usted probablemente ha dibujado un trillón de funciones lineales al crear gráficos. La función lineal que es más probable encontrarse con en el examen es f (x) = mx + b.

En los gráficos, m es la pendiente de la línea - la cantidad que la línea se mueve hacia adelante y hacia arriba o hacia abajo. los b es donde la línea atraviesa, o se cruza, el y-eje. He aquí un típico PSAT / NMSQT pregunta sobre funciones lineales:

¿Cuál de los siguientes gráficos representa una función lineal?

En primer lugar, recordar que función lineal en realidad sólo significa que la función es una línea recta cuando se hace un gráfico, lo que significa que tiene una pendiente constante. Una manera de resolver este problema es pensar en la pendiente entre cada par de puntos en cada gráfico. En Choice (A), los dos primeros puntos son (-2, -2) y (-1, -4).

Usted puede pensar en pendiente como aumentando en ejecución o como cambio en y por el cambio en x. En este caso, cuando X consigue 1 grande (-2 a -1), y 2 consigue más pequeña (de -2 a -4), lo que significa que la pendiente es

Ahora comparación de los dos puntos siguientes, (-1, -4) y (1, 4). En este caso, X obtiene 2 más grande y y 8 consigue más grande, haciendo una pendiente de

Pendiente diferente, por lo que estos tres puntos no hacen una línea.

Adelante a Choice (B)! Los dos primeros puntos, (-2, 3) y (-1, 0), tienen una pendiente de -3, y los dos siguientes puntos, (-1, 0) y (1, 0), tienen una pendiente de 0 . Ahora echa un vistazo a Choice (C): La pendiente entre (-2, 10) y (-1, 8) es -2 y entre (-1, 8) y (1, 4) también es -2. Ooh!

Sigue para ver si -2 es la pendiente para los próximos puntos así: (1, 4) y (2, 2) tener una pendiente de -2, y (2, 2) y (4, -2) también tienen una pendiente de -2. Éxito! La opción (C) es la correcta.

Funciones lineales aparecen en el mundo, también, no sólo en el examen. Por ejemplo, la tarifa que pagar para viajar en un tren puede variar dependiendo de la distancia que vaya. En una ciudad en particular, su tarifa del metro depende del número de paradas que usted viaje. Usted paga 50 centavos para cualquier viaje, y luego un adicional de 25 centavos por cada parada que viaja.

Usted puede modelar el costo de un viaje en metro como c = 0,50 + 0,25X, dónde c es el costo de la carrera, y X es el número de paradas que usted viaja.

Listo para tratar algunas cuestiones de función? Aqui tienes:

1. ¿Cuál de estos puntos se encuentra en la línea, si

   

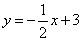
   (A) (- 1, 5)(B) (0, 2)(C) (1, 3)(D) (2, 2)(E) (4, 2)

2. ¿Cuál es la ecuación de la recta que pasa por los puntos (1, 5) y (3, 6)?

   

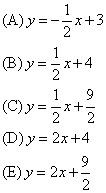
Ahora compruebe sus respuestas:

1. D. (2, 2)

   Para cada par ordenado, sólo tiene que enchufar el X-valor en el X en la ecuación y ver si el y-valor que se sale coincide con el y-valor en el par ordenado. Si lo hace, has encontrado tu respuesta! Un truco aquí es ver que X será dividido por 2, por lo que cualquier extraño X-valor no tendrá un número entero y-valor emparejado con ella, lo que elimina las opciones (A) y (C).

   Prueba de opción (B) es fácil - enchufe X = 0 y se obtiene y = 3, no el y-valor en la respuesta. En Choice (D), de enchufar X = 2 y obtener y = 2 como la salida - exactamente lo que usted está esperando! La opción (D) que es.

2. C.

   

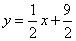
   Su primer paso debe ser encontrar la pendiente de la línea:

   

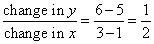
   que se estrecha sus respuestas a Choice (B) o (C). Para determinar qué contestar es, enchufe 1 por X y comprobar si el y valor que se sale es 5.

Funciones cuadráticas se muestran como y = ax² + bx + c o f (x) = ax² + bx + c. Usted no tiene que hacer mucho con funciones cuadráticas, simplemente interpretar gráficos. (Se ven como la nariz de un avión, mirando hacia abajo desde arriba.)