Determinar la distribución de los datos financieros
Se puede medir la forma en que los datos se distribuyen en torno a la media de varias maneras diferentes. Obviamente, no todos los números en un conjunto de datos van a ser exactamente el mismo que el de la media. Digamos que el ingreso neto promedio de una corporación es de $ 10.000. Eso está muy bien, pero no te dice si ese número cambia mucho.
La corporación puede ganar muy consistente $ 10.000 cada año, o puede ganar $ 0 en el año anterior y $ 20.000 al año siguiente. Esta información es el tipo de cosas vale la pena conocer, y se puede medir de varias maneras.
Rango es muy simple-es simplemente la diferencia entre el mayor y los valores más pequeños. Así, si una empresa tuvo ganancias de $ 10.000 y $ 20.000, entonces se puede decir que tenía un rango de dos años de $ 10,000, o el 100 por ciento.
Si usted fuera a mirar en el rango de los ingresos de la corporación en los últimos 20 años, es posible que desee prestar atención a su rango intercuartil (el rango del 50 por ciento de los valores) para asegurarse de que la corporación no experimentó ganancias inusualmente altos o bajos en ciertos años, lo que deshacerse de sus datos.
Para encontrar el rango intercuartil, se tomaría las ganancias de todos los años y ponerlos en orden numérico, divida en cuatro partes iguales, y luego simplemente toma el rango de las medias de dos piezas. Por lo tanto, si las ganancias de una empresa tenían un rango de $ 100.000, pero un rango intercuartílico de sólo $ 20.000, usted puede pensar que la corporación tenía cierta dispersión extrema en sus ganancias en algunos de esos años.
En los gráficos, estos rangos de frecuencia se ilustran en un par de maneras. Para comparar los cambios en los intervalos de tiempo especificados, diagramas de caja se utilizan a menudo para mostrar los cambios en la media y la distribución de los datos financieros, mientras que las tendencias de cambio en la dispersión se incluyen con frecuencia en las bandas de Bollinger. (La figura ilustra la media, máxima y los valores mínimos en un intervalo en el tiempo.)
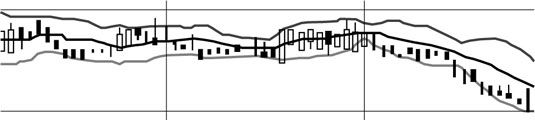
La desviación estándar, otra medida de la distribución, esta vez representado por la letra # 963- (sigma), es un concepto que se utiliza con bastante frecuencia en las ecuaciones, y así es como se calcula que:
Calcule la media.
Por ejemplo:
1, 2, 3, 4, 5 Mean = 3
Resta cada valor de la media
Por ejemplo:
3-1 = 2 3-2 = 1 3-3 = 0, y así sucesivamente
Cuadrados cada una diferencia.
Por ejemplo:
22= 4, 12= 1, 02= 0, -12= 1, -22= 4
Añadir los cuadrados juntos.
Por ejemplo:
4 + 1 + 0 + 1 + 4 = 10
Divida el resultado por el número de valores.
Por ejemplo:
10/5 = 2
Toma la raíz cuadrada de la respuesta de la Etapa 5
Por ejemplo:
# 8730-2 = 1,41
Por lo tanto, la desviación estándar es de 1.41. Eso significa que la dispersión de los valores de distancia de la media se mide en unidades por valor de 1,41 cada uno.
-
Los diagramas de caja: técnica gráfica de datos estadísticos -
¿Cuánto propagación es allí en los datos? -
Excel 2007 el análisis de datos para dummies -
3 maneras de describir las poblaciones y muestras en las estadísticas empresariales -
Aplicando la regla empírica (68-95-99,7) a un conjunto de datos estadísticos - Los conjuntos de datos y problemas de estadística descriptiva
El empleo de la regla empírica en problemas estadísticos La regla empírica en las estadísticas establece que para una distribución normal, casi todos los datos caerán dentro de tres desviaciones estándar de la media. Use la regla empírica para resolver los siguientes problemas.Ejemplos de…
Cómo calcular la varianza y la desviación estándar en la distribución uniforme los distribución uniforme se utiliza para describir una situación en la que todos los posibles resultados de un experimento aleatorio tienen la misma probabilidad de ocurrir. Puede utilizar la varianza y la desviación estándar para medir el…
¿Cómo encontrar el rango intercuartil para una muestra estadística Para obtener una medida de la variación sobre la base del resumen de cinco números de una muestra estadística, usted puede encontrar lo que se llama la rango intercuartil, o IQR.El propósito del resumen de cinco números es dar la estadística…
Cómo detectar la variabilidad estadística en un histograma Usted puede tener una idea de la variabilidad en un conjunto examinado su histograma de datos estadísticos. Por ejemplo, si los datos son todos iguales, todos ellos están colocados en una sola barra, y no hay variabilidad. Si una cantidad igual de…
¿Cómo se utilizan los valores z en las estadísticas Si un conjunto de datos estadísticos tiene una distribución normal, se acostumbra a estandarizar todos los datos para obtener puntuaciones estándar conocido como z-valores o z-puntajes. La distribución de z-valores adquiere una distribución…
Medidas de dispersión Central Medidas de dispersión centrales muestran cómo "extienden" los elementos de un conjunto de datos son de la media. Tres de las medidas más utilizadas de dispersión central son los siguientes:RangoVarianzaDesviacion estandarRangolos alcance de un…
Información general de las técnicas gráficas Existen diferentes tipos de gráficos pueden ser útiles para el análisis de datos. Estos incluyen diagramas de tallo y hojas, gráficos de dispersión, diagramas de caja, histogramas, cuantil-cuantil (QQ) parcelas y parcelas de autocorrelación.LA…
La desviación estándar y la varianza Los problemas aquí se centran en calcular, interpretar y comparar la desviación estándar y la varianza en las estadísticas básicas. Resuelve los siguientes problemas sobre la desviación estándar y la varianza.Ejemplos de preguntas¿Qué mide…
Estadísticas términos para saber cuando se utiliza Excel 2007 las herramientas de análisis de datos Con las herramientas de análisis de datos disponibles en Excel 2007, puede crear hojas de cálculo que muestran los detalles de cualquier estadística se puede crear una fórmula para encontrar - y usted puede encontrar cualquier número. Es bueno…
Estadísticas para grandes datos para los maniquíes Medidas de tendencia central muestran el centro de un conjunto de datos. Tres de las medidas más utilizadas de tendencia central son la media, la mediana y la moda.SignificarSignificar es otra palabra para la media. Esta es la fórmula para el…
La elección de la justa medida de dispersión en psicología estadística Las medidas de dispersión que utiliza en psicología estadística que muestran la dispersión o variabilidad de la variable que se está midiendo. Los tres principales son la gama, el rango intercuartil y la desviación estándar.Familiarización…
Psicología estadística para los maniquíes (edición uk) En psicología estadística, estudios de investigación que impliquen la recolección datos cuantitativos (todos los datos que se puede contar o representa como números) por lo general requieren que usted pueda recoger y almacenar datos en una hoja…