Cómo utilizar el modelo de Markov en el análisis predictivo

los Modelo de Markov es un modelo estadístico que se puede utilizar en el análisis predictivo que se basa en gran medida en la teoría de la probabilidad. (Es el nombre de un matemático ruso cuya investigación primaria era en teoría de la probabilidad.)

He aquí un escenario práctico que ilustra cómo funciona: Imagina que quieres predecir si Team X va a ganar el partido de mañana. Lo primero que debe hacer es recoger estadísticas anteriores sobre el Team X. La pregunta que podría surgir es lo lejos que debe ir en la historia?

Vamos a suponer que fueron capaces de llegar a los últimos 10 resultados del juego del pasado en secuencia. ¿Quieres saber la probabilidad de Team X ganar el próximo partido, teniendo en cuenta los resultados de los últimos 10 partidos.

El problema es que cuanto más atrás en la historia que quieras ir, más difícil y más complejo el cálculo de recopilación de datos y probabilidad convertirse.

Lo creas o no, simplifica el modelo de Markov su vida que le proporciona la Markov Asunción, que se parece a esto cuando usted lo escribe en palabras:

La probabilidad de que un evento ocurra, dado n eventos pasados, es aproximadamente igual a la probabilidad de que un evento que va a suceder dado sólo el último evento pasado.

Escrito como una fórmula, el Markov Asunción se ve así:

De cualquier manera, el Markov Asunción significa que usted no tiene que ir muy atrás en la historia para predecir el resultado de mañana. Usted sólo puede utilizar el evento pasado más reciente. Esto se llama el primer orden predicción Markov porque usted está considerando sólo el último evento de predecir el futuro evento.

LA segundo orden de predicción de Markov incluye sólo los últimos dos eventos que suceden en secuencia. A partir de la ecuación que acabamos de dar, la siguiente ecuación ampliamente utilizado también puede ser derivada:

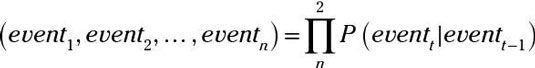
Esta ecuación tiene como objetivo para calcular la probabilidad de que algunos eventos sucederán en secuencia: evento₁ después evento₂, etcétera. Esta probabilidad puede ser calculada multiplicando la probabilidad de cada evento_t (dado el caso anterior a ella) por el siguiente evento en la secuencia. Por ejemplo, suponga que desea para predecir la probabilidad de que el Team X gana, pierde, y luego los lazos.

Así es como funcionaría un modelo predictivo típico basado en un modelo de Markov. Consideremos el mismo ejemplo: Supongamos que desea predecir los resultados de un partido de fútbol que se jugará por el Team X. Los tres resultados posibles - llamada estados - son triunfo, pérdida, tratamiento o empate.

Suponga que usted ha recogido datos estadísticos anteriores sobre los resultados de los partidos de fútbol del equipo X, y que el Team X perdió su último juego. Usted quiere predecir el resultado del próximo partido de fútbol. Todo es cuestión de adivinar si Team X va a ganar, perder o empatar - basándose únicamente en los datos de los juegos anteriores. Así que aquí es cómo se utiliza un modelo de Markov para hacer esa predicción.

1. Calcula unas probabilidades basadas en datos del pasado.

   Por ejemplo, ¿cuántas veces ha Team X perdido juegos? ¿Cuántas veces ha Team X ganado partidos? Por ejemplo, imagine si el Equipo X ganó 6 partidos fuera de diez partidos en total. Entonces, el equipo X ha ganado 60 por ciento del tiempo. En otras palabras, la probabilidad de ganar para el equipo X es 60 por ciento.

2. Calcular la probabilidad de una pérdida, y entonces la probabilidad de un lazo, de la misma manera.

3. Utilice la Na # 239-ve ecuación de probabilidad de Bayes para calcular las probabilidades como las siguientes:

   

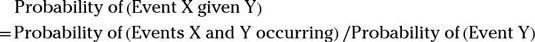
4. La probabilidad de que el Team X va a ganar, ya que el equipo X perdió el último partido.

5. La probabilidad de que el Team X perderá, ya que el equipo X ganó el último partido.

6. Calcular las probabilidades para cada estado (triunfo, pérdida, tratamiento o empate).

7. Suponiendo que el equipo juega solamente un juego por día, las probabilidades son como sigue:

8. P (Win | Pérdida) es la probabilidad de que el Team X va a ganar hoy en día, dado que perdió ayer.

9. P (Win | Tie) es la probabilidad de que el Team X va a ganar hoy en día, ya que empató ayer.

10. P (Win | Win) es la probabilidad de que el Team X va a ganar hoy en día, ya que ganó ayer.

11. Utilizando las probabilidades calculadas, crear un gráfico.

    Un círculo en este cuadro representa un posible estado que el Team X podría alcanzar en un momento dado (victoria, derrota, empate) - los números de las flechas representan las probabilidades de que el Team X podría pasar de un estado a otro.

    

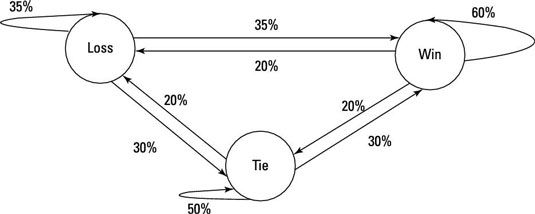
Por ejemplo, si el Equipo X acaba de ganar el juego de hoy (su estado actual = victoria), la probabilidad de que el equipo va a ganar otra vez es 60 por ciento- la probabilidad de que van a perder el próximo partido es el 20 por ciento (en cuyo caso ' d pasar del estado actual = ganar al futuro Estado = pérdida).

Suponga que quiere conocer las posibilidades que el Team X ganará dos partidos seguidos y perder el tercero. Como se pueden imaginar, eso no es una predicción sencilla de hacer.

Sin embargo, el uso de la tabla recién creada y la asunción de Markov, se puede predecir fácilmente las posibilidades de que tal evento ocurra. Se empieza con el estado victoria, caminar por el estado victoria de nuevo, y grabar 60 porcentaje entonces se mueve al estado de pérdidas y grabar 20 por ciento.

Las posibilidades de que el equipo X ganará dos veces y perder el tercer partido convertido en fácil de calcular: 60 veces 60 veces ciento por ciento del 20 por ciento, que es el 60 por ciento del 60 por ciento * * 20 por ciento, lo que equivale a 72 por ciento.

¿Cuáles son las posibilidades de que el equipo X ganará, a continuación, atar, y luego de perder dos veces después de eso? La respuesta es 20 por ciento (pasando de estado victoria para empatar estado) veces el 20 por ciento (pasando de lazo a la pérdida), los tiempos de 35 por ciento (pasando de la pérdida de la pérdida) veces el 35 por ciento (pasando de la pérdida de la pérdida). El resultado es 49 por ciento.