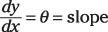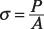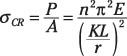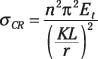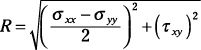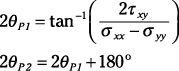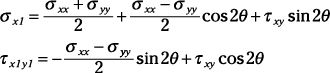Cuando se trata de la mecánica de materiales, la elección de la fórmula correcta para calcular la tensión en un punto dado puede ser difícil. Tensiones normal y cortante vienen en una amplia variedad de aplicaciones, cada aplicación de estrés con su propia fórmula de cálculo. Los tipos de estrés más comunes que tratamos en mecánica básica de los materiales se dividen en varias categorías principales:
Tensión axial: LARED es igual al área bruta de la sección transversal menos los agujeros que puedan existir.
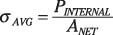
De paredes delgadas recipientes a presión: Existen dos tensiones: una tensión axial a lo largo del eje del elemento y un aro (o radial) la tensión, que se produce tangencial al radio de la sección transversal. Estas tensiones se basan en la presión manométrica p en el interior del recipiente a presión.
por recipientes a presión cilíndricos, use este par de fórmulas:
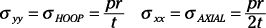
Para recipientes a presión esféricos, utilice la siguiente fórmula:
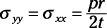
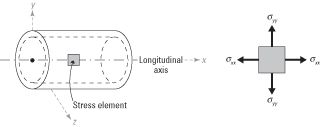
Esfuerzos de flexión: Para secciones simétricas en el plano XY, utilice esta fórmula:
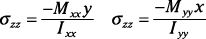
(momento de la X-eje) (momento de la y-eje)
Tensiones de cizallamiento a la flexión: Ésta es la fórmula para el cálculo de esfuerzo cortante a la flexión:
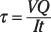
Esfuerzo cortante torsional: Utilice esta fórmula para hallar esfuerzo cortante torsional:
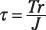
Mecánica básica de Materiales: Informática Destaca en Columnas
Saber cómo calcular la tensión en una columna (miembro de compresión) Es un punto básico de conocimientos en mecánica de materiales. Determinar si la columna es "corto, delgado, o intermedio calculando su máxima relación de esbeltez (KL / r). Para las columnas cortas, el estrés de un miembro en compresión es la formulación básica esfuerzo axial. Para las columnas intermedias y delgadas, se puede utilizar la ecuación de pandeo del generalizado de Euler. Relaciones de esbeltez aproximados de columnas de acero se muestran entre paréntesis.
Las columnas cortas: Relación de esbeltez (KL / r lt; 50).
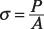
Esbeltas columnas: Relación de esbeltez (KL / r # 8805-200). El cálculo para esbeltas columnas utiliza el módulo de elasticidad (E).
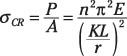
Columnas intermedias: Relación de esbeltez (50 # 8804- KL / r lt; 200). La fórmula para columnas intermedias utiliza el módulo de elasticidad tangencial (Et).
El uso del círculo de Mohr Encontrar tensiones principales y ángulos
Cualquier persona en las ciencias mecánicas probablemente familiarizado con Mohr's círculo - una técnica gráfica útil para encontrar tensiones principales y las tensiones en los materiales. Círculo de Mohr también le indica los principales ángulos (orientaciones) de las tensiones principales sin tener que conectar un ángulo en ecuaciones de transformación estrés.
A partir de un elemento de tensión o deformación en el plano XY, construir una red con una tensión normal en el eje horizontal y un esfuerzo cortante en la vertical. (. Parcelas de estrés de cizalla positivos en la parte inferior) Luego sólo tienes que seguir estos pasos:
Trazar la cara vertical coordina V (sigmaxx , tauxy).
Trazar las coordenadas H horizontales (sigmayy, -tauxy).
Se utiliza el signo opuesto de la tensión de cizallamiento de la Etapa 1 debido a que los esfuerzos de corte en las caras horizontales están creando un par que los saldos (o actúa en la dirección opuesta de) las tensiones tangenciales en las caras verticales.
Dibuja una línea de diámetro de conexión Puntos V (del paso 1) y H (del paso 2).
Dibuja el círculo alrededor del diámetro de la Etapa 3.
El círculo debe pasar a través de puntos V y H como se muestra.
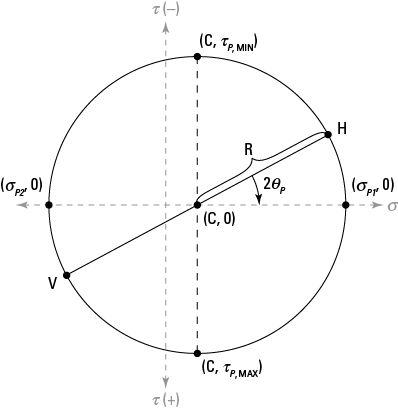
Calcular la posición normal de estrés para el punto central del círculo (C).
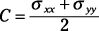
Calcular el radio (R) para el círculo.
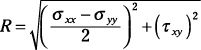
Determinar las tensiones principales sigmaP1 y sigmaP2.
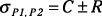
Calcular los principales ángulos Theta-P1 y Theta-P2.
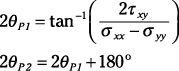
También puede utilizar las ecuaciones directamente (en lugar del círculo de Mohr) para determinar las tensiones transformadas en cualquier ángulo:
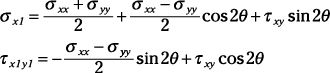
Para construir un círculo de Mohr para la cepa o para utilizar las ecuaciones de transformación, sustituto épsilonxx para sigmaxx, épsilonyy para sigmayy, y (0.5)gammaxy para tauxy en las ecuaciones anteriores.
Usando una Ley de Hooke generalizada de Tensiones
En la mecánica de materiales, Hooke'ley s es la relación que conecta tensiones a las cepas. Aunque ley original de Hooke fue desarrollado para tensiones uniaxiales, puede utilizar una versión generalizada de la ley de Hooke para conectar el estrés y la tensión en los objetos tridimensionales, también. Finalmente, la ley de Hooke le ayuda a relacionarse tensiones (que se basan en las cargas) a cepas (que se basan en las deformaciones).
Para un estado tridimensional de estrés, la cepa normal en una dirección dada (por ejemplo, X) Es una función de las tensiones en las tres direcciones ortogonales (por lo general el cartesiano X-, y-, y zdirecciones), como se muestra por esta ecuación:
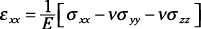
dónde E es el módulo de elasticidad y # 957- es el coeficiente de Poisson para el material. Para una tensión uniaxial, dos de las tensiones en la ecuación son cero. Para una condición de estrés biaxial, una de las tensiones en esta ecuación es cero.
La relación generalizada de la ley de Hooke para cizallamiento en el plano XY se puede dar como
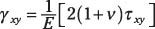
Mecánica de los Materiales: Cálculo Deformaciones de Cargas
Deformaciones medir la respuesta de una estructura bajo una carga, y el cálculo de que la deformación es una parte importante de la mecánica de los materiales. Cálculos de deformación vienen en una amplia variedad, dependiendo del tipo de carga que provoca la deformación. Deformaciones axiales son causadas por cargas axiales y ángulos de giro son las causas por las cargas de torsión. La curva elástica para elementos sometidos a flexión es en realidad una ecuación diferencial.
La siguiente lista muestra algunas de las expresiones más utilizadas deformación que te encuentres en la mecánica de los materiales:
Deformación axial:
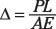
Ángulo de giro de torsión:
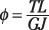
El doble de la integración de encontrar deformaciones de vigas:
Usted puede aproximar y(X), la ecuación de la curva elástica como una función de X, por la siguiente ecuación diferencial:
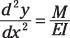
Usted necesita encontrar primero la ecuación de momento generalizado M en todos los lugares a lo largo de la viga como una función de la posición X. Resuelva esta ecuación mediante la integración de dos veces y la aplicación de las condiciones de contorno para resolver constantes de integración (desplazamientos de apoyo conocido (y) Y rotaciones (# 952-). Recuerda,