Análisis de circuitos y las ecuaciones de malla corrientes

Análisis de malla de corriente

(análisis de bucle de corriente) Puede ayudar a reducir el número de ecuaciones que debe resolver durante el análisis de circuitos. Análisis de malla de corriente no es más que la ley de voltaje de Kircholff adaptado para los circuitos que tienen muchos dispositivos conectados en múltiples bucles.

Analizar circuitos de dos mallas

Esta sección le guía a través del análisis de malla de corriente cuando se tienen dos ecuaciones, una para Malla Una y otra para Malla B. En el circuito de la muestra que se muestra aquí, ambas mallas tienen una corriente en sentido horario.

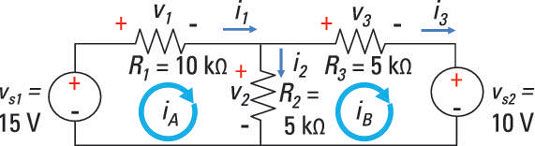
El siguiente paso es aplicar KVL de malla A y B para llegar a las siguientes ecuaciones de malla:

A continuación, escriba las corrientes de dispositivos en términos de corrientes de malla. Luego de expresar las corrientes de dispositivos en términos de las corrientes de malla utilizando la ley de Ohm:

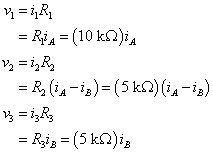
Ahora usted puede sustituir los valores de tensión anteriores en las ecuaciones KVL que encontraste anteriormente:

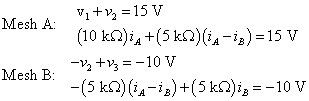
Al reorganizar las ecuaciones anteriores para ponerlos en forma estándar, se obtiene

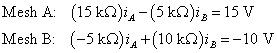
La conversión de estas ecuaciones de malla en forma de matriz en los resultados

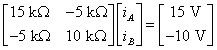
La ecuación anterior tiene la forma Hacha = b, donde la matriz LA es los coeficientes de resistencias, X es un vector de corrientes de malla desconocidos, y b es un vector de fuentes de tensión independientes.

Usted puede utilizar su calculadora gráfica o software matriz para darle las corrientes de malla:

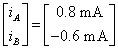
Con estas corrientes de malla calculados, usted puede encontrar las corrientes de dispositivos:

yo₁ = yo_LA = 0,8 mAyo₂ = yo_LA - yo_B = 0,8 mA - (-0,6 mA) = 1,4 mA

Para completar el análisis, tapar las corrientes de dispositivos y resistencias en ecuaciones ley de Ohm. Usted encontrará las siguientes tensiones de dispositivos:

v₁ = yo₁R₁ = (0,8 mA) (10 k # 937-) = 8 Vv₂ = yo₂R₂ = (1,5 mA) (5 k # 937-) = 7 Vv₃ = yo₃R₃ = (-0,6 MA) (5 k # 937-) = -3 V

Las tensiones de dispositivos anteriores tienen sentido porque satisfacen KVL para cada malla.

Analizar circuitos con tres o más mallas

Usted puede solicitar un análisis de malla de corriente cuando se trata de circuitos que tienen tres o más mallas. El proceso es el mismo que para circuitos con sólo dos corrientes de malla. Considere este circuito de muestreo, que muestra las tensiones y corrientes para cada uno de los dispositivos, así como las corrientes de malla yo_LA, yo_B, y yo_C. Observe que todas las corrientes de malla fluyen en sentido horario.

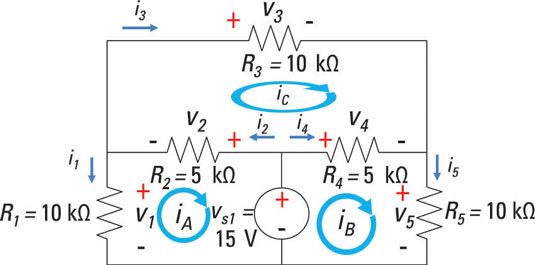
Las ecuaciones KVL para mallas A, B, y C son

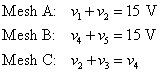
Ahora expresar las corrientes de dispositivos en términos de corrientes de malla. A continuación, aplicar la ley de Ohm para obtener los voltajes de elementos en términos de las corrientes de malla:

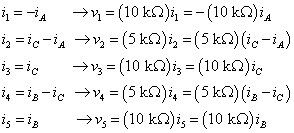
Al sustituir los voltajes de dispositivos anteriores en las ecuaciones KVL encontrado antes, que terminan con

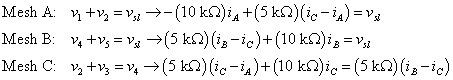
Reorganizar las ecuaciones para ponerlos en forma estándar. Puede insertar algunos ceros como términos de marcador de posición para ayudar a configurar las matrices en el siguiente paso:

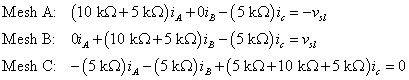
Y usted puede traducir estas ecuaciones de forma estándar en forma de matriz para obtener

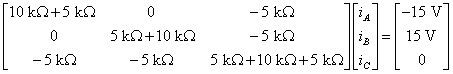
Simplificar los elementos de la matriz de resistencia:

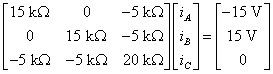
Nótese que en la matriz de resistencia, los valores principales diagonal son todos positivos, los valores fuera de la diagonal son todos negativos o cero, y los valores fuera de la diagonal son simétricas. Para un circuito con una fuente independiente, que la simetría con respecto a la diagonal principal es una buena señal de que ha configurado correctamente el problema.

Usted puede utilizar su calculadora gráfica o software de la matriz de encontrar las corrientes de malla:

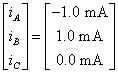
El actual yo_C = 0 tiene sentido debido a la simetría del circuito. Con estos valores calculados para corrientes de malla, a encontrar las siguientes corrientes de dispositivos:

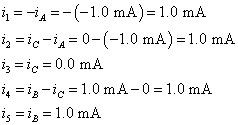
Para completar el análisis, el cálculo de las tensiones de dispositivos utilizando la ley de Ohm, que relaciona las corrientes y voltajes de dispositivos:

Los resultados anteriores tienen sentido porque satisfacen las ecuaciones KVL para las tres mallas.