El concepto de propagación de errores

Una forma menos extrema del viejo dicho "la basura en igual basura" es "difusa en iguales salir borrosa." Fluctuaciones al azar en una o más variables medidas producen fluctuaciones aleatorias en nada a calcular a partir de esas variables. Este proceso se llama la propagación de errores. Usted necesita saber cómo la medición errores se propagan a través de un cálculo que se realiza en una cantidad medida.

Aquí hay una forma sencilla de calcular el SE de una variable (Y) Que se calcula a partir de casi cualquier expresión matemática que implica una sola variable (X). Comenzando con el observado X valor (Xo), Y su error estándar (SE), Acaba de hacer el siguiente cálculo de 3 pasos:

1. Evaluar la expresión, sustituyendo el valor de Xo - SE para X en la fórmula. Llame el resultado Y₁.

2. Evaluar la expresión, sustituyendo el valor de Xo + SE para X en la fórmula. Llame el resultado Y₂.

3. los SE de Y es simplemente (Y₂ - Y₁) / 2.

He aquí un ejemplo que muestra cómo (y por qué) funciona este proceso.

Supongamos que usted mide el diámetro (d) De una moneda como 2,3 centímetros, utilizando una pinza o una regla que usted sabe (de la experiencia pasada) tiene una SE de # 177- 0,2 centímetros. Ahora dice que desea calcular el área (LA) De la moneda a partir del diámetro medido.

Si usted sabe que el área de un círculo está dada por la fórmula

se puede calcular inmediatamente la zona de la moneda como

que se puede hacer ejercicio en su calculadora para obtener 4.15475628 centímetros cuadrados. Por supuesto, nunca se daría un informe sobre la zona a que muchos dígitos porque no mide el diámetro de forma muy precisa. Así lo precisa es su área calculada? En otras palabras, ¿cómo hace eso # 177- 0,2 centímetros SE de d propagarse a través de la fórmula para darle el SE de LA?

Una forma de responder a esta pregunta sería considerar un margen de error (ME) alrededor del diámetro observado (d) Que va de un SE abajo d a uno por encima de SE d. El ME es siempre dos PE amplia. En el ejemplo de la moneda, ME del diámetro se extiende desde 2,3 hasta 0,2 a 2,3 + 0,2, o de 2,1 a 2,5 centímetros.

Ahora averiguar las áreas correspondientes a los diámetros en los extremos inferior y superior de la ME. Uso de 2,1 para d en el área de la fórmula da LA = 3.46, y el uso de 2,5 para d da LA = 4.91. Así que el ME para el área de la moneda va de 3,46 a 4,91 centímetros cuadrados.

El ancho de esta ME es 4,91 - 3,46, o 1,45 centímetros cuadrados, lo que representa dos SES para la zona. Así que el SE de la zona es 1,45 / 2, o 0.725 centímetro cuadrado.

La línea curva representa la fórmula LA = # 960- / 4) x d². Las flechas oscuras muestran cómo el diámetro medido (2,3 centímetros), cuando se conecta a la fórmula, produce un área calculada de aproximadamente 4,15 centímetros cuadrados. Las flechas grises de color más claro representan los extremos inferior y superior de la ME y muestran cómo el ME para el diámetro produce un ME para la zona.

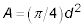
El SE de la zona depende de la SE del diámetro y la pendiente de la curva. De hecho, el SE de la zona es igual a la SE del diámetro multiplicado por la pendiente de la curva.

Desafortunadamente, el simple procedimiento se ilustra en este ejemplo no se puede generalizar para manejar las funciones de dos o más variables, tales como el cálculo de índice de masa corporal de una persona de altura y peso.

Los matemáticos han derivado una fórmula muy general para el cálculo de (aproximadamente) de cómo las PE en una o más variables se propagan a través de cualquier expresión que implique esas variables, pero es muy complicado, y para usarlo hay que ser realmente bueno en cálculo o es casi seguro cometer errores en el camino.

Afortunadamente, hay alternativas mucho mejores:

• Puede utilizar algunas fórmulas de errores de propagación simples expresiones simples.

• Aún más fácil, usted puede ir a una página web que hace los cálculos de errores de propagación para las funciones de una o dos variables.

• Puede utilizar un enfoque muy general de simulación que puede analizar fácilmente cómo los errores se propagan a través de incluso las expresiones más complicadas, que implica cualquier número de variables.