Mostrar respuesta en frecuencia de un circuito con diagramas de Bode
Para estudiar una gama de frecuencias, se utiliza diagramas de Bode. Diagramas de Bode ayudan a visualizar cómo polos y ceros afectan la respuesta de frecuencia de un circuito. Usted puede expresar la ganancia respuesta de frecuencia |T (jomega-)
Conteúdo
Por ejemplo, si la ganancia es |T (jomega-)|, La ganancia en decibeles es 40 dB. También, una ganancia de 1 es 0 dB.
En la frecuencia de corte omega-C, que se define comúnmente como TMAX / Radic-2, tiene el siguiente ganancia:
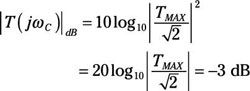
Por lo tanto, la frecuencia de corte también se conoce como el punto de -3 dB o el punto medio-Power.
¿Por qué? Debido a que el conjunto anterior de ecuaciones que implican una función de transferencia puede ser visto como el cuadrado de la tensión o bien la función de transferencia actual. La cuadratura la función de transferencia le da la relación de poder entre la señal de salida y de entrada se transforma debido a que el cuadrado de la tensión o la corriente es proporcional al poder.
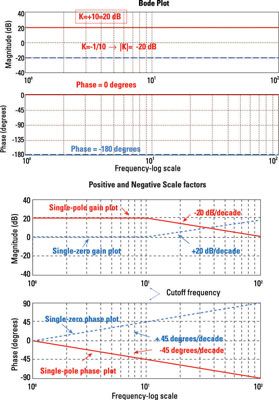
Las parcelas de registro de frecuencia de la ganancia |T (jomega-)| y la fase theta- (omega-) son llamados Diagramas de Bode, o Diagramas de Bode.
Una trama básica Bode
Diagramas de Bode vienen en pares para describir la respuesta de frecuencia de los circuitos. Por lo general, usted tiene
Una ganancia gráfico log-frecuencia en decibelios dada en el diagrama de la parte superior
Un diagrama de fase de registro de frecuencia en grados dada en el diagrama inferior
Aquí está una parcela de muestreo Bode.
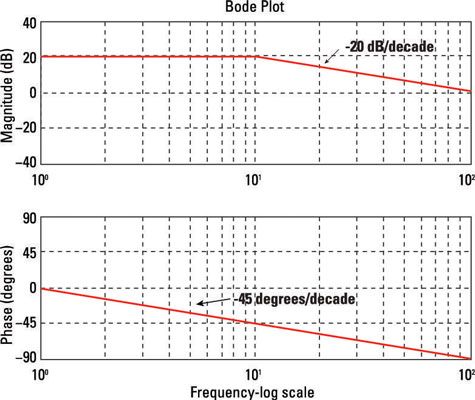
El eje horizontal por lo general viene en una de las siguientes escalas de registro de frecuencia, normalmente décadas:
Octavas: Una octava tiene un rango de frecuencias cuyo límite superior es el doble del límite inferior (2: 1 ratio). Por ejemplo, la voz por lo general oscila entre 2 kHz a 4 kHz, que comprende aproximadamente 1 octava.
Décadas: Una década tiene una gama con una proporción de 10: 1. Por ejemplo, el oído humano por lo general oscila entre 20 Hz a 20 kHz (20-103 Hz), por lo que se extiende por 3 décadas.
Polacos, ceros y factores de escala: parcelas Retratando Bode de funciones de transferencia
La mayoría de las veces, se utiliza el software de ingeniería para dibujar diagramas de Bode. Pero se puede aproximar diagramas de Bode a mano - o por lo menos el aviso cuando la trama generada por computadora está en mal estado - si usted entiende cómo los polos y ceros de la función de transferencia dan forma a la respuesta de frecuencia. Los polos, por supuesto, son las raíces de denominador de la función de transferencia, y ceros son las raíces de su numerador.
Esta tabla muestra algunas reglas básicas, aproximados que tener en cuenta al examinar las funciones de transferencia y diagramas de Bode.
| Característico de la función de transferencia, T (jugrave-) | Efectos sobre la Ganancia Solar, |T (jugrave-)|dB | Efectos en la Fase de Terreno, jedB |
|---|---|---|
| Factor de escala (ganancia) | Cambia toda la trama de ganancia arriba o hacia abajo sin cambiar las frecuencias de corte (esquina) | La fase de Bode es un-afectada si el factor de escala es positiva. Si el factor de escala es negativo, la fase de Bode cambia en ± 180 °. |
| Polo real | Presenta una pendiente de -20 dB / década para la ganancia de Bode, a partir de la frecuencia de polo | La fase de Bode rueda fuera en una pendiente de -45 ° / década. La fase en el polo es -45 °. Para frecuencias superiores a 10 veces la frecuencia de polo, el ángulo de fase aportado por un solo polo es de aproximadamente -90 °. |
| Cero real | Presenta una pendiente de 20 dB / década para la ganancia de Bode, a partir de la frecuencia cero | La fase de Bode rueda fuera en una pendiente de + 45 ° / década. La fase en el cero es + 45 °. Para frecuencias superiores a 10 veces la frecuencia cero, el ángulo de fase aportado por un solo cero real es de aproximadamente + 90 °. |
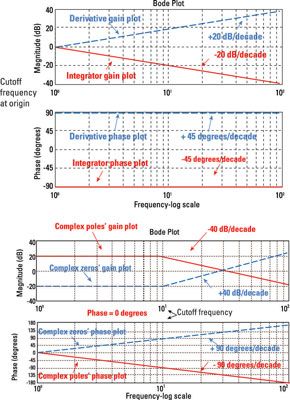
| Integrador | Presenta un polo real en el originario de un poste real en el origen (un integrador 1 /s) Tiene una pendiente ganancia de -20 dB / década que pasa por 0 dB a omega- = 1 | El ángulo aportado por un integrador es -90 ° en todas las frecuencias. |
| Diferenciador | Presenta un cero real en el originario un cero en el origen (un diferenciador) tiene una pendiente de 20 dB de ganancia / década que pasa a través de al 0 dB a ugrave- = 1 | El ángulo aportado por un diferenciador es + 90 ° en todas las frecuencias. |
| Complejo par de polos | Proporciona una pendiente de -40 dB / década | La fase de Bode parcela tiene una pendiente de -90 ° / década. La fase a la frecuencia de polos complejos es -90 °. Para frecuencias mayores que 10 veces la frecuencia de corte, el ángulo de fase aportado por un complejo de par de polos es de aproximadamente -180 °. |
| Complejo par de ceros | Proporciona una pendiente de 40 dB / década | La fase de Bode parcela tiene una pendiente de + 90 ° / década. La fase a la frecuencia cero es complejo + 90 °. Para frecuencias mayores que 10 veces la frecuencia de corte, el ángulo de fase aportado por un complejo par de ceros es de aproximadamente + 180 °. |
-
Cómo establecer la frecuencia de muestreo en Logic Pro x -
Cómo graficar secuencias y diagramas de fase en TI-Nspire -
Cómo ajustar las frecuencias en itunes -
Cómo utilizar fasores para el análisis de circuitos -
Crear paso banda y banda de rechazo filtros con circuitos en paralelo RLC -
Crear pasa banda y filtros con circuitos en serie RLC banda rechazar
Componentes de la electrónica: cómo utilizar un amplificador operacional como un amplificador de ganancia unitaria LA amplificador de ganancia unitaria es un circuito amplificador electrónico que no amplifica. En otras palabras, tiene una ganancia de 1. La tensión de salida en un amplificador de ganancia unidad es la misma que la tensión de entrada.Usted…
Componentes de la electrónica: el op amp ideales Si usted lee sobre amplificadores operacionales en la web o en un libro electrónico, usted, sin duda, se encuentra con el término amplificador operacional ideal. Un amplificador operacional ideales es un amplificador operacional hipotética con…
Generalizar la impedancia de ampliar la ley de Ohm para condensadores e inductores Utilizar el concepto de impedancia al gernalize ley de Ohm en forma fasorial para que pueda aplicar y extender la ley de condensadores e inductores. Después de describir la impedancia, utilice diagramas fasoriales para mostrar la diferencia de fase…
¿Cómo describir la respuesta de frecuencia de los circuitos de filtro Circuitos de filtro (como los filtros de paso bajo, filtros de paso alto, filtros de paso de banda y banda rechazan filtros) forma al contenido de frecuencia de las señales, permitiendo solamente ciertas frecuencias para pasar a través. Puede…
Análisis de S-dominio: la comprensión de polos y ceros de f (s) Transformadas de Laplace se pueden utilizar para predecir el comportamiento de un circuito. La transformada de Laplace toma una función de dominio de tiempo f (t), y la transforma en la función F (s) en el s-dominio. Puede ver las transformadas de…
Funciones sinusoidales y análisis de circuitos Las funciones sinusoidales (seno y coseno) aparecen por todas partes, y juegan un papel importante en el análisis de circuitos. Las funciones sinusoidales proporcionan una buena aproximación para describir la entrada de un circuito y el…
Conexión de polos y ceros geometría y la respuesta de frecuencia: un vídeo En el estudio de los sistemas, tanto en tiempo continuo y tiempo discreto, la respuesta de frecuencia y su relación con el polo y cero lugares en el s- y z-aviones, respectivamente, son de importancia fundamental.Este video útiles presenta el…
Señales y sistemas en tiempo continuo Señales y sistemas en tiempo continuo nunca toman un descanso. Cuando un circuito está cableado arriba, una señal está allí para tomar, y el sistema comienza a trabajar - y no se detiene. Tenga en cuenta que el término señal se utiliza aquí…
11 señales y sistemas conceptos utilizados para diseñar un ecualizador gráfico de audio A continuación se presentan señales y sistemas once conceptos que se aplican al diseño de un sistema de procesamiento de señal conocida como una ecualizador gráfico de audio. Cuando usted escucha la música en un reproductor de música…
¿Cómo caracterizar el filtro corrector para un ecualizador gráfico de audio Un filtro de pico para un ecualizador gráfico de audio proporciona una ganancia o pérdida (atenuación) a una frecuencia central específica Fc. Un filtro de pico tiene magnitud de frecuencia unidad respuesta, o 0 dB de ganancia, a frecuencias muy…
Cómo utilizar pylab diferenciales LCC y ecuaciones en diferencias Herramientas informáticas juegan un papel importante en las señales y los sistemas modernos de análisis y diseño. LCC diferencial y ecuaciones en diferencias son una parte fundamental de los sistemas simples y de alta complejidad.…
Señales y sistemas matemáticas cobra vida con aplicaciones de animación Usted no puede apreciar completamente la matemática de señales y sistemas en su primer encuentro. Para mejorar su comprensión, puede utilizar la animación por ordenador para dar vida a algunos de los conceptos más difíciles y espero hacer una…