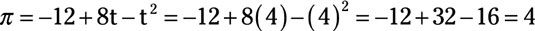Cómo calcular los plazos de investigación y desarrollo en economía de la empresa
Un factor importante que influye en los costos de investigación y desarrollo es la cantidad de tiempo que toma para la finalización del proyecto. Un marco de tiempo más corto tiende a aumentar el costo de investigación y desarrollo, ya que requiere más recursos y salidas en falso que resulta en esfuerzos inútiles son más probables. Por lo tanto, existe una relación inversa entre el tiempo y los costos de investigación y desarrollo. los función disyuntiva tiempo-costo describe esta relación entre el tiempo y coste de desarrollo.
Además del tiempo-costo trade-off en el costo de desarrollo, el potencial de ingresos netos de un proyecto también se ve influida por el tiempo. Debido a que otras empresas también innovan, existe la posibilidad de que su innovación hace que su proyecto de investigación y desarrollo obsoleto. Por lo tanto, un proyecto de desarrollo de corta duración es probable que tenga mayores ingresos netos.
En base a estos dos elementos, es necesario determinar el período de tiempo óptimo para la finalización del proyecto. El momento óptimo maximiza el beneficio - la diferencia entre los ingresos netos y la función de compensación de tiempo-costo.
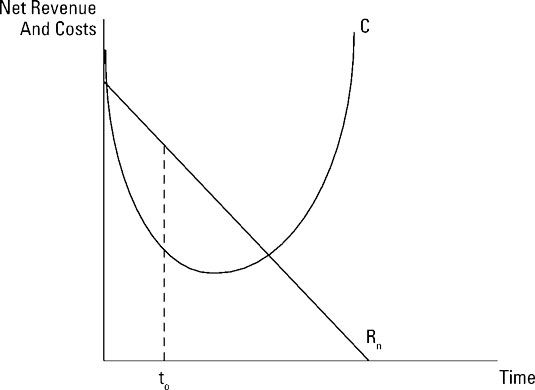
Usted quiere elegir un lapso de tiempo (t) para el proyecto que maximiza el beneficio - la diferencia entre los ingresos netos (Rn) Y el costo de desarrollo (C). El lapso de tiempo óptimo en la ilustración se representa por t0 ya que maximiza la diferencia entre los ingresos netos (Rn) Y el costo de desarrollo (C). Estos se muestra por la gran brecha o diferencia vertical entre estas dos líneas.
El ingreso neto esperado, Rn, de su investigación y desarrollo de proyectos iguales
dónde Rn representa los ingresos netos en millones de dólares y t es el tiempo medido en años.
Su función disyuntiva tiempo-costo es
dónde C es el costo de desarrollo de millones de dólares y t es de nuevo el tiempo.
Con el fin de determinar el marco de tiempo óptimo para la finalización del proyecto, tome las siguientes medidas:
Tenga en cuenta que el beneficio esperado, # 240-, desde el proyecto es igual a los ingresos netos menos el costo de desarrollo representado por la función de compensación de tiempo-costo.
Por lo tanto,
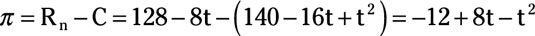
Con el fin de maximizar el beneficio, tome la derivada de lucro, # 240-, con respecto al tiempo, t.
Este derivado es igual
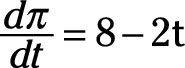
Establezca la igualdad derivada a cero y resolver para t.
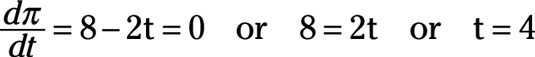
Por lo tanto, el marco de tiempo óptimo del proyecto es de cuatro años. Sustituyendo t es igual a 4 en la ecuación beneficio esperado indica que el beneficio esperado es de $ 4 millones.
-
Cómo participación en las ganancias puede mejorar el rendimiento de un gerente de negocios -
Cómo calcular el costo esperado del desarrollo de nuevos productos en la economía de la empresa -
Cómo calcular el beneficio económico -
Cómo calcular el máximo beneficio en un monopolio -
Cómo calcular el valor actual con el valor temporal del dinero -
Cómo determinar que el ingreso marginal es igual al costo marginal
Cómo maximizar los beneficios mediante los ingresos totales y el costo total El beneficio total es igual al ingreso total menos el costo total. Con el fin de maximizar el beneficio total, debe maximizar la diferencia entre el ingreso total y el costo total. Lo primero que debe hacer es determinar la cantidad que maximiza el…
¿Cómo maximizar los márgenes de beneficio teniendo en cuenta Para maximizar los beneficios mediante el ingreso marginal y el costo marginal, que se centran en la contribución de una unidad adicional de producción hace que a su ingreso en relación con su contribución a su costo.El ingreso marginal es el…
Cómo maximizar las ganancias con las unidades marginales Muy a menudo es más fácil determinar la cantidad que maximiza los beneficios de la producción, centrándose en la última unidad que produce, o la unidad marginal. Con el fin de añadir a su beneficio, una unidad adicional o marginal del bien…
Cómo maximizar el beneficio con el costo total y los ingresos Economía de la empresa permite a las empresas para calcular el precio de un producto que maximizar las ganancias. Para ello, necesitan el ingreso total y el costo total. Los ingresos totales es igual al precio multiplicado por la cantidad vendida,…
Cómo maximizar el beneficio con derivados Usted puede usar el cálculo para maximizar la ecuación de ganancia total. Debido a que los ingresos totales y el costo total se expresaron en función de la cantidad, a determinar la cantidad que maximiza los beneficios de la producción mediante…
Cómo minimizar las pérdidas a través de la economía empresarial Por desgracia, no siempre es el caso que el beneficio de la empresa es positivo. Sin embargo, las empresas pueden seguir produciendo en el corto plazo con el fin de minimizar las pérdidas. Es importante recordar que las empresas que cerraron en el…
Economía de la empresa: cómo maximizar el beneficio a corto plazo en la competencia monopolística Economistas gerenciales han estudiado la competencia monopolística para entender cómo maximizar el beneficio en ese modelo económico. Debido a que una empresa en competencia monopolística produce un bien diferenciado, la maximización de…
Economía de la empresa: cómo determinar cuándo apagar Hay un punto en el que debe dar de inmediato y cerrar su negocio. Pero primero hay que recordar que el ir a la quiebra en el corto plazo no significa que sus pérdidas van a cero. Debido a que algunos de los insumos que emplean son fijos, salir de…
Cómo determinar el costo marginal, el ingreso marginal y el beneficio marginal en la economía El costo marginal, el ingreso marginal y beneficio marginal todos implican la cantidad de una función sube (o hacia abajo) a medida que avanza más de 1 hacia la derecha - esto es muy similar a la forma en que las obras de aproximación…
Calcula npv con una serie de flujos de efectivo futuros Se espera que la mayoría de proyectos de capital para proporcionar una serie de flujos de efectivo durante un período de tiempo. Los siguientes son los pasos individuales necesarios para calcular el VAN cuando se tiene una serie de flujos de caja…
Relaciones costo-volumen-beneficio para la contabilidad de gestión Contabilidad de gestión proporciona herramientas útiles, tales como las relaciones costo-volumen-beneficio, para ayudar a la toma de decisiones. El análisis de costo-volumen-utilidad le ayuda a entender las diferentes formas de satisfacer las…
Calcular la relación de beneficio para una empresa Negocio está motivada por el lucro, por lo que el cálculo de la tasa de beneficios para que una empresa es muy importante, por decir lo menos. El resultado final no se llama la línea de fondo sin una buena razón. La tasa de beneficios indica la…