Cómo dividir un segmento de línea en varias partes
Si usted puede encontrar el punto medio de un segmento, se puede dividir en dos partes iguales. Encontrar el centro de cada una de las dos partes iguales permite encontrar los puntos necesarios para dividir todo el segmento en cuatro partes iguales. Encontrar el centro de cada uno de estos segmentos le da ocho partes iguales, y así sucesivamente.
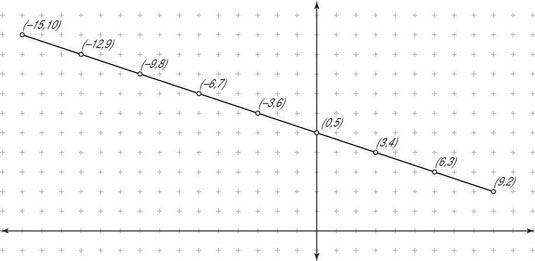
Por ejemplo, para dividir el segmento con puntos finales (-15,10) y (9,2) en ocho partes iguales, encontrar los distintos puntos medios, así:
El punto medio del segmento principal de (-15,10) a (9,2) es (3,6).
El punto medio de la mitad del segmento principal, a partir de (-15,10) a (3,6), es (-9,8), y el punto medio de la otra mitad del segmento principal, a partir de (-3,6 ) a (9,2), es (3,4).
Los puntos medios de los cuatro segmentos determinados anteriormente son (-12,9), (6,7), (0,5), y (6,3).
La figura muestra las coordenadas de los puntos que dividen este segmento de línea en ocho partes iguales.
Utilizando el método del punto medio está bien, siempre y cuando lo que desea es dividir un segmento en un número par de segmentos iguales. Pero su trabajo no siempre es tan fácil. Por ejemplo, puede que tenga que dividir un segmento en tres partes iguales, cinco partes iguales, o algún otro número impar de partes iguales.
Para encontrar un punto que no es equidistante de los extremos de un segmento, sólo tiene que utilizar la siguiente fórmula:
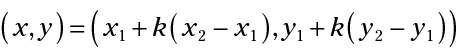
En esta fórmula, (X1,y1) Es el punto final en el que está comenzando, (X2,y2) Es el otro punto final, y k es la parte fraccionaria del segmento que desea.
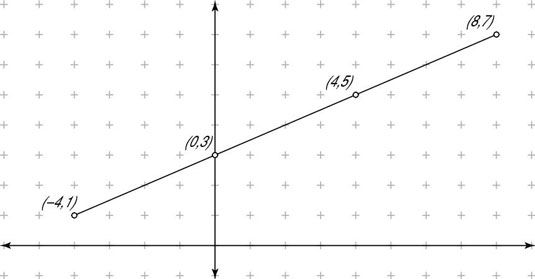
Por lo tanto, para encontrar las coordenadas que dividen el segmento con puntos finales (-4,1) y (8,7) en tres partes iguales, en primer lugar encontrar el punto de que es un tercio de la distancia a partir de (-4,1) a la otra punto final y, a continuación, encontrar el punto de que es dos tercios de la distancia de (-4,1) en el otro extremo. Los pasos siguientes muestran cómo.
Para encontrar el punto de que es un tercio de la distancia a partir de (-4,1) al otro punto final, (8,7):
Reemplazar X1 con -4, X2 con 8, y1 con 1, y2 con 7, y k con 1/3.
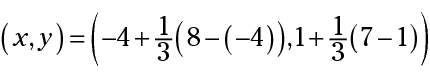
Restar los valores en los paréntesis interiores.
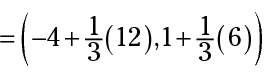
Haga la multiplicación y luego agregar los resultados para obtener las coordenadas.
= (- 4 + 4,1 + 2) = (0,3)
Para encontrar el punto de que es dos tercios de la distancia a partir de (-4,1) al otro punto final, (8,7):
Reemplazar X1 con -4, X2 con 8, y1 con 1, y2 con 7, y k con 2/3.
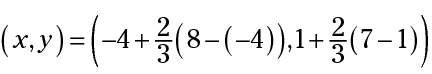
Restar los valores en los paréntesis interiores.
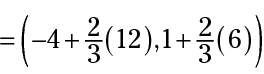
Haga la multiplicación y luego agregar los resultados para obtener las coordenadas.
= (- 4 + 8,1 + 4) = (4,5)
La siguiente figura muestra la gráfica de este segmento de la línea y los puntos que lo dividen en tres partes iguales.
-
Cómo conectar líneas con polilínea en AutoCAD 2014 -
Cómo conectar un segmento recto a un segmento de la curva en Photoshop CS6 -
Cómo construir un punto medio con la TI-84 Plus -
Cómo construir objetos geométricos en la TI-Nspire -
Cómo dividir números en la recta numérica -
Conceptos básicos de álgebra necesarios para pre-cálculo
Bisectriz y trisecar segmentos Bisección y trisección implican cortar algo en dos o tres partes iguales. Si eres un fan de las bicicletas y los triciclos y bifocales y trifocales - por no mencionar el biatlón y el triatlón, bifurcación y trifurcación y bipartición y…
Construir líneas y segmentos en jr Cabri. La aplicación de geometría Cabri Jr. para las ofertas de la calculadora TI-84 Plus Crear y Construcción menús que contienen una gran cantidad de herramientas. Con estas herramientas se pueden hacer cosas mundanas tales como líneas de construir,…
Cómo calcular el área de un polígono regular LA polígono regular es equilátero (tiene lados iguales) y equiangular (tiene ángulos iguales). Para encontrar el área de un polígono regular, se utiliza un apotema - un segmento que une el centro del polígono al punto medio de cualquier lado y…
Cómo determinar el área de sectores y segmentos de un círculo Marque una sección de un círculo con un arco y una cuerda, y usted tiene un segmento (este tipo de segmento tiene nada que ver con un segmento de línea). Lanzar un par de radios alrededor de un arco, y usted tiene un sector.Así que aquí están…
Cómo medir segmentos de línea Para encontrar la medida o el tamaño de un segmento, sólo tiene que medir su longitud. ¿Qué más se puede medir? Después de todo, la longitud es la única característica tiene un segmento. Tienes tu resumen, su medio y sus segmentos largos.…
Trabajar con definiciones, teoremas y postulados Definiciones, teoremas y postulados son los componentes básicos de las pruebas de geometría. Con muy pocas excepciones, todas las justificaciones en la columna de la razón es una de estas tres cosas. La siguiente figura muestra un ejemplo de una…
Cifras trigonométricas básicas Segmentos, rayos y líneas son algunas de las formas básicas que se encuentran en la geometría, y son casi tan importantes en trigonometría. Utiliza esos segmentos, rayos y líneas para formar ángulos.Dibujo segmentos, rayos y líneasLA segmento…
Acordes frente tangentes de los círculos Usted muestra el diámetro y el radio de un círculo dibujando segmentos a partir de un punto en el círculo, ya sea hacia oa través del centro del círculo. Sin embargo, otras dos figuras rectas tienen un lugar en un círculo. Una de estas figuras…
¿Cómo encontrar el punto medio de un segmento de línea En medio de un segmento de línea es su punto medio. Para encontrar el punto medio de un segmento de línea, que acaba de calcular los promedios de las coordenadas - fácil como pastel.El punto medio, M, de un segmento con puntos finales (X1,y1) Y…
Cómo localizar el centro de un círculo Una forma de describir el centro de un círculo es identificar la centroide. Este punto medio es el centro de gravedad, donde se puede equilibrar el triángulo y girar a su alrededor.Al graficar un círculo, triángulo, o segmento de línea mediante…
Cómo localizar el centro de un triángulo Si dibuja líneas de cada esquina (o vértice) De un triángulo para el punto medio de los lados opuestos, entonces esas tres líneas se encuentran en un centro, o centroide, del triángulo. El centro de gravedad es el centro del triángulo de la…
Coordinar preguntas de práctica de geometría en el acto El examen de matemáticas ACT contiene preguntas sobre la geometría analítica, que requieren que usted sabe cosas como las fórmulas de punto medio y la distancia de puntos en un X, y-coordinar gráfico. Aquí hay un par de ejemplos para que usted…