Cómo utilizar gráficos de control para seis sigma

El control estadístico de procesos primarios (SPC) herramienta para iniciativas Six Sigma es la gráfico de control

- un seguimiento gráfica de un proceso de entrada o una salida en el tiempo. En el gráfico de control, estas mediciones orugas se comparan visualmente a los límites de decisiones calculadas a partir de las probabilidades de los resultados reales del proceso.

La comparación visual entre los límites de decisión y los datos de rendimiento le permite detectar cualquier variación extraordinaria en el proceso - la variación que puede indicar un problema o cambio fundamental en el proceso.

Los diferentes tipos de gráficos de control se dividen en dos grandes categorías, dependiendo de qué tipo de medición del proceso que estés seguimiento: gráficos de control de datos continuos y atributos de datos gráficas de control. Aquí está una lista de algunos de los gráficos de control más comunes que se utilizan en cada categoría en Six Sigma:

• Continua gráficos de control de datos:

• Promedios y rangos

  

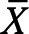
• Promedios y las desviaciones estándar

  

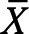
• Los valores individuales y rangos móviles

  

Atributo gráficos de control de datos:

p gráfico

u gráfico

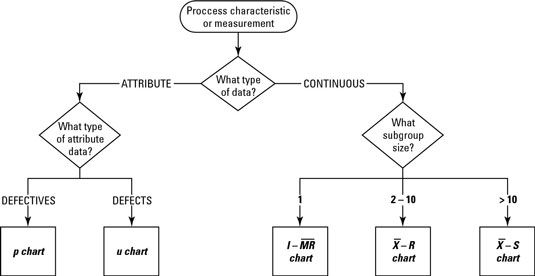
El gráfico de control que elija siempre se basa primero en el tipo de datos que tiene y luego en su objetivo de control. El árbol de decisiones gráfico de control le ayuda en su decisión.

El enfoque general paso a paso para la ejecución de un gráfico de control es el siguiente:

1. Definir lo que necesita ser controlada o supervisada.

2. Determinar el sistema de medición que suministrará los datos.

3. Establecer los gráficos de control.

4. Correctamente recopilar datos.

5. Tomar decisiones apropiadas sobre la base de información de la carta de control.

   

Los gráficos de control que proporcionan información sobre el proceso de medida que está trazando de dos maneras: la distryobución del proceso y la tendencias o el cambio del proceso en el tiempo. Utilice los gráficos de control de

• Proporcionar un lenguaje sencillo, común para discutir el comportamiento y el rendimiento de un proceso de las entradas o medida de salida

• Controlar el cumplimiento de un proceso por el saber cuándo y cuándo no actuar

• Reducir la necesidad de la inspección

• La capacidad de entender y predecir proceso basado en las tendencias y otros puntos de vista de rendimiento

• Determinar si los cambios realizados en el proceso están teniendo el resultado deseado

• Proporcionar una visión permanente, continua del desempeño del proceso

• Crear un repositorio de datos para las actividades de mejora de seguimiento en

Supervisar el proceso de

Lo que se mide se logró. Decidir qué medir y gestionar en Six Sigma está determinada por su Definir, Medir, Analizar, Mejorar y (DMAI) actividad del proyecto antes de llegar a la fase de control.

En pocas palabras, lo que monitorizar con gráficos de control son el insumo crítico Xs y los CTQs salida a descubrir en su proyecto. Estos son los que mueven los hilos en el proceso que se alinean con las necesidades de su cliente. En la fase de control, a supervisar las salidas - los CTQs - y controlar las entradas, el crítico Xs. Cuando se hace correctamente, este control le permite beneficiarse de sus esfuerzos.

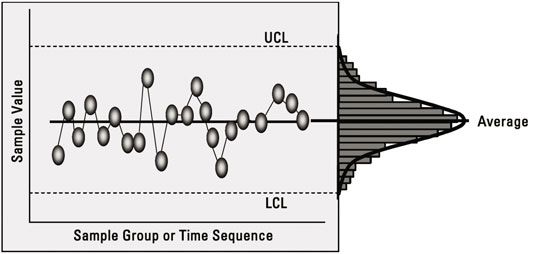
Los gráficos de control son gráficos bidimensionales de trazado el rendimiento de un proceso en un eje, y el tiempo o la secuencia de muestras de datos en el otro eje. Estos gráficos trazan una secuencia de puntos de datos medidos a partir del proceso. También puede ver la secuencia de puntos como una distribución.

Los gráficos de control tienen los siguientes atributos determinados por los propios datos:

• Un promedio o línea central de los datos: Es la suma de todos los datos de entrada dividido por el número total de puntos de datos.

• Un límite de control superior (UCL): Es típicamente tres desviaciones estándar proceso por encima del promedio.

• Un límite de control inferior (LCL): Es típicamente tres desviaciones estándar proceso de debajo de la media.

  

Entender los límites de control

Usted puede preguntar, " Cuál es el significado de un límite de control, y de dónde viene desde "? La sencillez de los límites de control, junto con sus poderosas implicaciones, le sorprenderá. Los gráficos de control uso probabilidad expresado como límites de control para ayudar a determinar si se espera una medida proceso observado que ocurra (en el control) o no se espera que ocurra, dada la variación normal proceso.

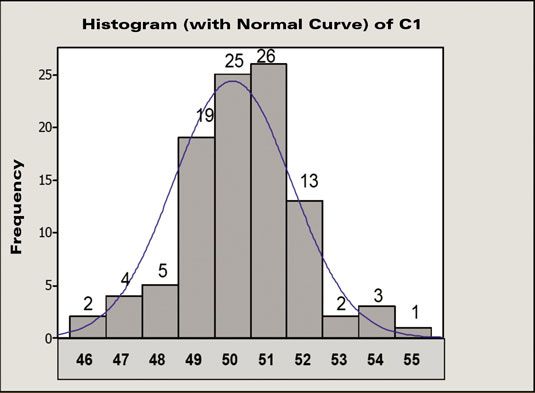
Datos de 25 puntos sobre 100 tienen un valor de 50. A continuación, estimar que la probabilidad de obtener un evento con un valor de 50 es de 25 sobre 100, o el 25 por ciento. Del mismo modo, la probabilidad de obtener un evento con un valor de 52 es de aproximadamente 13 por ciento y para valores de 55 y por encima de, la probabilidad es mucho menor.

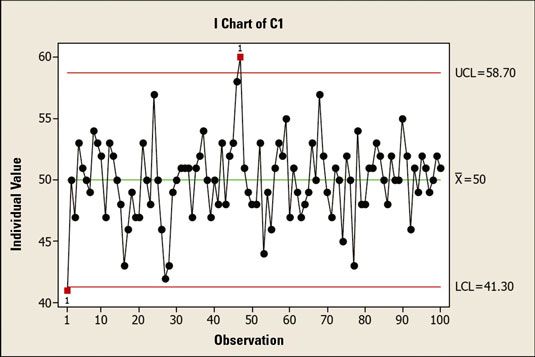
El límite superior de control de 58,7 es de tres desviaciones estándar por encima de la media. El límite inferior de control de 41,3 es de tres desviaciones estándar por debajo de la media. Más o menos tres desviaciones estándar de la media incluye 99.7 por ciento de todos los datos de una población normalmente distribuida.

Por lo tanto, usted tiene un 99,7 por ciento de probabilidad de que un punto de datos de proceso caerá entre estos dos límites. Eso significa que tiene solamente una ocasión de 0,3 por ciento que una medición estará por encima de la UCL o por debajo de la LCL.

En el siglo 20, Walter Shewhart, uno de los fundadores del movimiento moderno de calidad, formalizó las ideas utilizadas en los gráficos de control. Definió que, si una medida cae dentro de más o menos tres desviaciones estándar de su media, se considera " esperada " comportamiento para el proceso.

Si una medida cae dentro de más o menos tres desviaciones estándar de su media, se considera " esperada " comportamiento para el proceso y por lo tanto es una causa común de variación. Variación de causa común resulta de la operación normal de un proceso y se basa en el diseño del proceso, las actividades del proceso, los materiales, y otros parámetros del proceso.

Sin embargo, si un punto de datos cae fuera de los límites de control, algo especial ha ocurrido con el proceso. En otras palabras, algo fuera de lo común ha hecho que el proceso de ir fuera de control. Esta situación se conoce como variación de causa especial, lo que significa que, basado en el comportamiento del proceso hasta ese punto, la probabilidad de que se produzca la situación es menos de 0,3 por ciento.

Una medida con una baja probabilidad tales sugiere que circunstancias especiales afectan el proceso. Este enfoque simple, cuantitativo mediante el uso de probabilidad es la esencia de todas las gráficas de control.