Cómo analizar la variación normal y probabilidad para seis sigma

Todos los datos de proceso y de producto en proyectos de Six Sigma tienen variación- cada instancia repetida de cualquier punto de datos medido es diferente de la instancia anterior. Y como el conjunto de medidas repetidas acumula, una forma comienza a formarse.

Datos reales generalmente se agrupan en torno a un valor central, y la aparición de puntos de datos cada vez más lejos del valor central disminuye. Esta configuración es la clase en forma de campana clásica de variación constantemente ejecuta a través.

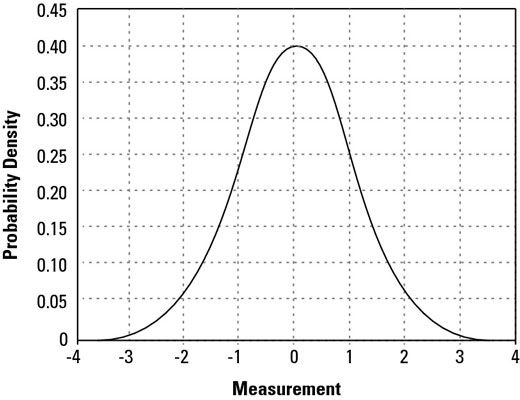
El modelo normal representa la densidad de todas las probabilidades de un proceso o producto típico - todas pasadas, actuales y futuras apariciones de la característica en su configuración actual.

El eje horizontal se escala para unidades de desviación estándar de la distribución. Y aunque la figura muestra solamente la curva de campana de -4 a +4 desviaciones estándar desviaciones estándar, de hecho, se extiende hasta el infinito negativo de la izquierda y todo el camino hasta el infinito positivo a la derecha.

El eje vertical mide la densidad de probabilidad para cada valor de la medición desde el infinito negativo a positivo infinity- cuanto mayor es la curva de la campana, mayor es la probabilidad de que el valor correspondiente en el eje horizontal que se produzcan.

Observe que la curva normal es siempre positiva, es decir, su valor nunca es cero o negativo. También es perfectamente symmetrical- si usted dobla la curva en su apogeo, las mitades derecha e izquierda coinciden perfectamente. El valor promedio - llamada # 956- para el modelo perfecto - se produce en el pico o el centro de la campana.

La desviación estándar - llamada # 963- para el modelo perfecto - es equivalente a la distancia horizontal desde el centro de la curva (la media, o # 956-) a cualquier punto de la curva donde sus forma cambia de cóncava a convexa. En la Figura 12-1, con la escala horizontal en unidades de desviaciones estándar, se puede ver que esta distancia se produce en los puntos de medición de -1 y 1.

Un último punto a tener en cuenta sobre el modelo normal es que, si se mide el área encerrada por la curva de campana y el eje horizontal, desde menos infinito hasta el infinito positivo, siempre es igual a 1. Es decir, el área total bajo la curva normal representa 100 por ciento de todas las posibilidades - con 50 por ciento caer encima de la media y 50 por ciento por debajo.

Trabajando desde el infinito negativo y positivo, si se calcula el área bajo la curva normal entre las desviaciones estándar -3 y +3, el resultado es 0,997, o el 99,7 por ciento de los posibles resultados de la característica proceso. Más lejos en, entre -2 y 2 desviaciones estándar, aproximadamente 95 por ciento se capturan todas las posibilidades. Y 68 por ciento de todas las posibilidades se encuentran entre -1 y +1 desviaciones estándar.

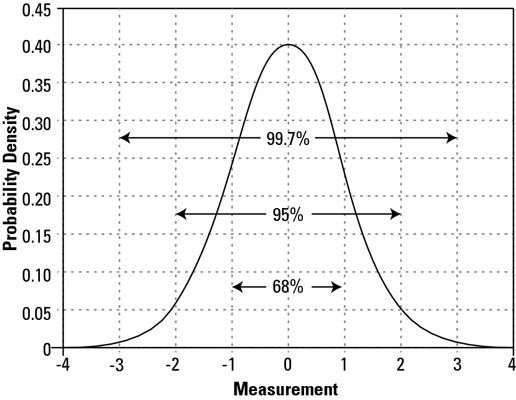
Debido a la simetría del modelo normal, puede utilizar estas mismas probabilidades de área para determinar las posibilidades que se encuentran más allá de los parámetros. Por ejemplo, debido a un 99,7 por ciento de todas las posibilidades de resultados se encuentran entre -3 y +3 desviaciones estándar, usted sabe que el 0,3 por ciento de posibilidades debe estar más allá de las desviaciones estándar -3 y +3, con 0,15 por ciento inferior a -3 desviaciones estándar y 0,15 por ciento mayor que +3 desviaciones estándar.

Y de manera similar, ya que aproximadamente el 95 por ciento de probabilidades se encuentran entre -2 y +2 desviaciones estándar, aproximadamente 5 por ciento de probabilidades debe estar más allá de las desviaciones estándar -2 y +2. En todos estos ejemplos, se puede ver que todas las posibilidades se combinan siempre al 100 por ciento.

Piense en un caso especial de la modelo normal, donde el promedio es igual a cero (# 956- = 0) y la desviación estándar es igual a uno (# 963- = 1). Una distribución normal con estos parámetros exactos se llama ninguna normardistribución normal.

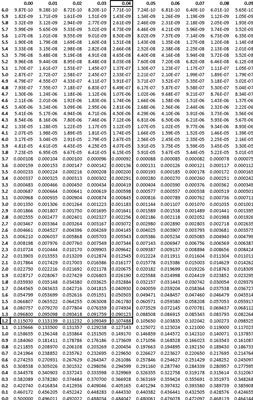
Los estadísticos han pasado mucho tiempo estudiando la distribución normal estándar. Una de las cosas importantes que han hecho es tabular el área bajo la curva normal estándar para varios valores de medición.

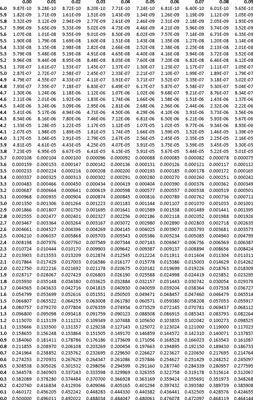
Las etiquetas de fila en el extremo izquierdo de esta tabla normal estándar corresponden a diferentes distancias más o menos del centro de cero de la distribución normal estándar. Las etiquetas de columna a través de la fila superior agregan un segundo decimal a las distancias. Los contenidos de las celdas se corresponden con la probabilidad más allá de la distancia especificada.

Cómo calcular la probabilidad encima o debajo de un valor único

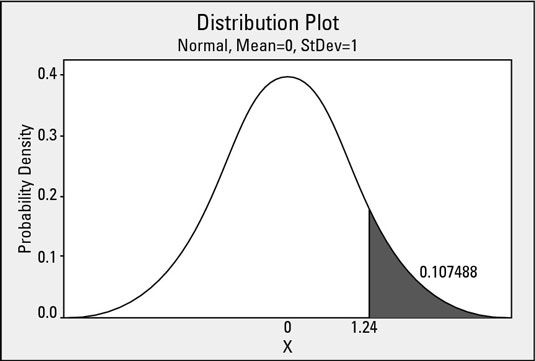
En las herramientas estadísticas de Six Sigma, que frecuentemente calcular probabilidades utilizando la tabla normal estándar. Por ejemplo, usted puede fácilmente buscar el área bajo la curva normal estándar superior a 1,24 en la tabla.

La probabilidad de la mesa es 0,107488. Por lo tanto, para una distribución normal con media de 0 y desviación estándar de 1, la probabilidad de observar un valor de datos mayor que 1,24 es 0,107488 (10,7 por ciento). Debido a la simetría del modelo, esta cifra es también la probabilidad exacta de observar un valor de menos de -1,24.

¡Pero eso no es todo! El uso de la idea de las probabilidades complementarias, se puede calcular un 1-0,107488 = 0,892512 (89,3 por ciento) probabilidad de observar una medición menos de 1,24 (ya la inversa, un 89,3 por ciento de probabilidad de observar una medida mayor que -1,24). Echa un vistazo a la figura 12-5 para ver estas probabilidades en acción.

Cómo calcular la probabilidad entre o fuera de dos valores

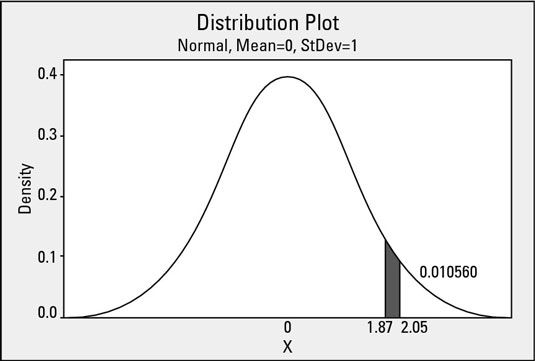
Averiguar las probabilidades de los valores individuales es relativamente simple. Averiguar la cantidad de área (probabilidad) es bajo la curva normal estándar entre dos valores finitos sólo es más difícil un poco. Por ejemplo, ¿cuál es el área bajo la curva normal estándar entre los valores de los ejes horizontales de 1,87 y 2,05?

Por lo demás, ¿cómo diablos se supone que debes determinar esa zona si sólo se puede buscar un valor de probabilidad en la tabla de probabilidad normal estándar a la vez?

Por otro lado, tiene una 1-,10560 = 0,89440 (89,4 por ciento) probabilidad de observar un valor fuera de este intervalo. Estas probabilidades se corresponden con una característica de proceso que tiene una media de 0 y una desviación estándar de 1.