Las estadísticas básicas que usted debe saber para el examen de certificación PMP

Para el examen de certificación PMP, usted necesitará saber algunos de terminología, medidas, y conceptos en la distribución. En primer lugar, ver algunas definiciones. A continuación, echar un vistazo a algunas estadísticas básicas.

Distribución de probabilidad. Una representación matemática o gráfica que representa la probabilidad de resultados diferentes a partir de un hecho fortuito.

Distribución normal. El distribución- la media, la mediana y la moda en forma de campana se encuentra con frecuencia son el mismo valor. También conocido como curva de campana o una Distribución gaussiana.

Distribución acumulativa. Una manera de graficar cualquier distribución para mostrar la probabilidad de que se alcanzarán un valor dado y menos (o más).

La media. También llamado el valor esperado, la media es el promedio de todos los puntos de datos. Media puede ser calculada como un promedio simple o una media ponderada, basada en un tipo específico de distribución de probabilidad, o mediante el uso de una simulación.

La mediana. El punto en la distribución donde el 50% de los resultados están por encima del valor, y el 50% de los resultados son inferiores al valor.

Modo. El punto de datos más frecuente.

Distribución triangular. Una distribución continua que se calcula mediante el uso de tres variables o de datos discretos puntos: optimista pesimista, y Lo más probable. No se ponderan en el cálculo de la media.

Distribución PERT. Una distribución continua se calcula mediante el uso de tres variables discretas: optimista pesimista, y Lo más probable, de los cuales Lo más probable se pondera en el cálculo de la media.

Para el examen, todas las preguntas se basan en una distribución normal. Aquí hay una curva de distribución normal.

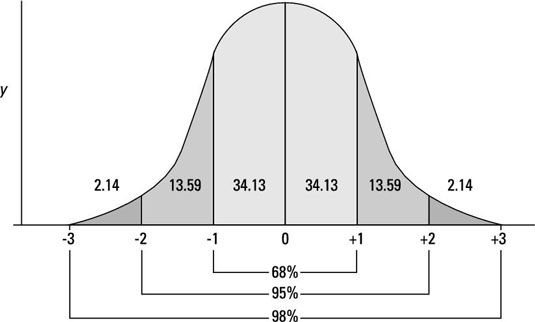
En una distribución normal, la media, la mediana y la moda son todos iguales. Ese es el punto más alto de la curva. Para una distribución normal, usted está buscando en dos aspectos: la media y la desviación estándar. La desviación estándar representa la distancia de un punto dado es de la media. También se llama sigma, o s. He aquí una definición más técnica:

Desviacion estandar. Una medida de la gama de resultados, la diferencia media de la media, calculado como la raíz cuadrada de la varianza. El símbolo para la desviación estándar es de # 963-.

La ecuación básica para el cálculo de la desviación estándar es de

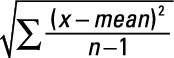
A los efectos del examen de PMP, puede utilizar un acceso directo. Sólo funciona para las distribuciones normales, sino porque eso es utiliza todo el examen de PMP, que debería estar bien. El acceso directo es

(pesimista - optimista) / 6

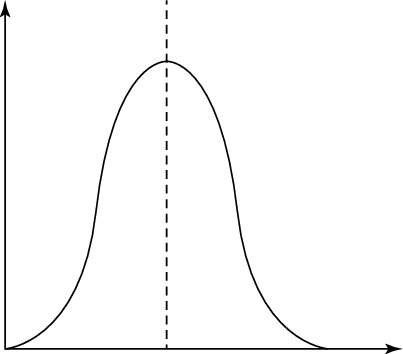
Básicamente, la media muestra la altura de la curva, y la desviación estándar determina la anchura de la curva. Una curva estrecha tiene una desviación estándar relativamente bajo. Una distribución más plana tiene una desviación estándar relativamente mayor.

Aquí está una amplia distribución.

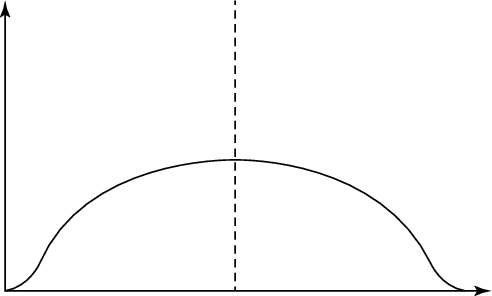
Generalmente, las mediciones se evaluaron por el número de desviaciones estándar son de la media. En una distribución normal

• 68,3% de los puntos de datos caen dentro de 1 desviación estándar.

• 95,5% de los puntos de datos caen dentro de 2 desviaciones estándar.

• 99,7% de los puntos de datos caen dentro de 3 desviaciones estándar.

Por lo tanto, para una distribución normal, casi todos los valores se encuentran dentro de 3 desviaciones estándar de la media.

Esta información es necesaria para la calidad, costo-estimación, duración, estimación y preguntas de riesgo en el examen PMP. Aquí está un ejemplo rápido sobre la calidad del proyecto en el que está opinando sobre la calidad de las estimaciones de duración.

Un miembro del equipo estima que la tarea A más probable es que se terminará en 30 días. El mejor de los casos es que podría estar terminado en 24 días, y el peor de los casos es que se tardaría 36 días. ¿Le gustaría estimaciones de finalización prevista. Con base en esta información, usted quiere saber la respuesta a esta pregunta:

¿Cuál es la probabilidad de que va a terminar la tarea en 28-32 días?

Para responder a esta pregunta, tome las siguientes medidas:

1. Calcula la media (valor esperado) mediante el uso de la ecuación de la distribución PERT.

   (24 + 4 (30) + 36) / 6 = 30

2. Calcula la desviación estándar mediante el uso de la fórmula breve.

   (36 - 24) / 6 = 2

3. Sumar y restar el valor de la desviación estándar hacia y desde la media.

   +/ -1# 963-es 28-32 días, lo que representa el 68%.

   Así, se puede estimar con fiabilidad una oportunidad 68% que la actividad estará terminado dentro de 28-32 días.

Aquí es una pieza más de la información que usted necesita saber: distribución acumulada. En una distribución acumulativa, verá lo siguiente:

• 0,15% de los puntos de datos caen entre 0 y # 963 -3-de la media.

• 2,25% de los puntos de datos caen entre 0 y -2 # 963-de la media.

• 16% de los puntos de datos caen entre 0 y -1# 963-de la media.

• 84% de los puntos de datos caen entre 0 y + 1 # 963-de la media.

• 97,75% de los puntos de datos caen entre 0 y + 2 # 963-de la media.

• 99,85% de los puntos de datos caen entre 0 y + 3 # 963-de la media.

Utilizando la misma pregunta, calcular la probabilidad de terminar en 32 días o menos.

Esta cuestión, sin embargo, se pregunta sobre la probabilidad acumulada de todos los valores de 32 días o menos. En el Paso 1 de la lista anterior, la media fue de 30 días. La desviación estándar fue de 2. Siga estos pasos para solucionar el problema:

1. 30 días (la media) + 1 # 243- (2 días) = ​​32 días.

2. En cuanto a la información anterior, se puede ver que el 84% de los resultados se encuentran entre 0 y + 1 # 243-de la media.

Por lo tanto, se puede estimar con fiabilidad una probabilidad del 84% que la tarea se terminará en 32 días o menos.

Debido a que el 68% de todos los resultados son +/- 1 # 963-de la media, si usted está tratando de determinar el porcentaje que es sólo + 1 # 963-o simplemente -1 # 963-, se divide 68% por 2 para obtener el 34%. Para obtener la distribución acumulada, se empieza con la media de 50% y añadir 34% para mostrar el valor acumulado de 1 # 963-:

50% + (68% / 2) = 84%

Puede restar 34% para obtener el valor acumulado de -1 # 963-:

50% - (68% / 2) = 16%

Usted sigue el mismo método para 2 # 963- utilizando 95,5% dividido por 2 y por 3 # 963-utilizando 99,7% dividido por 2.