Identidades recíprocas
Una gran ventaja de expresiones trigonométricas y ecuaciones es que se puede ajustar en tantas formas que se adaptan a sus necesidades. Las identidades recíprocas básicos aquí son los que la gente usa más frecuentemente.
Echa un vistazo a la primera identidad recíproca y su contraparte:
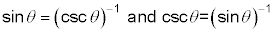
y
Una forma alternativa de escribir estas identidades utiliza un exponente de # 8210-1 en lugar de una fracción:
Tenga en cuenta que los exponentes se aplican a toda la función. Estas no son las funciones inversas:
Secante, cosecante y cotangente son técnicamente las tres funciones recíprocas, pero usted puede escribir identidades para mostrar sus inversos, también. Siguiente son la segunda identidad recíproca y su contraparte.
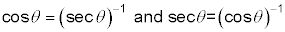
y
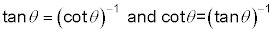
Una vez más, otra forma de escribir éstos es utilizar un exponente de -1. Los paréntesis se utilizan para asegurarse de que reconoce que este es el recíproco, no a la inversa.
La tangente y su recíproco, al menos, tienen nombres que suenan igual. Las otras dos funciones básicas y sus recíprocos (ver las ecuaciones anteriores) no parecen tener nombres que no están tan bien relacionados.
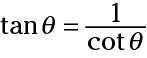
y
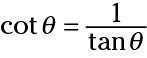
Y, para acabar con la notación alternativa:
-
Incluso identidades y pico en las funciones trigonométricas -
Primeros pasos con identidades trigonométricas -
Cómo calcular un ángulo usando funciones trigonométricas recíprocas -
¿Cómo demostrar una igualdad usando identidades recíprocas -
¿Cómo demostrar una igualdad usando identidades co-función -
¿Cómo demostrar identidades trigonométricas cuando se suman o restan términos
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
¿Cómo simplificar una expresión utilizando identidades de función co- Si usted toma la gráfica de y = Sen X y desplazar hacia la izquierda por pi / 2 unidades, se ve exactamente como la gráfica de y = Cos X. Lo mismo es cierto para la tangente y cotangente, así como secante y cosecante. Esa es la premisa básica de…
¿Cómo simplificar una expresión utilizando identidades recíprocas Cuando se le pregunta para simplificar una expresión que implica cosecante, secante o cotangente, cambia la expresión de funciones que implican seno, coseno, tangente o, respectivamente. Al cambiar las funciones de esta manera, usted está…
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
Una tabla rápida para las tres funciones trigonométricas recíprocas Funciones recíprocas tienen valores que son recíprocos, o voltea, de los valores de sus respectivas funciones. El recíproco de seno es cosecant, por lo que cada valor de la función es la inversa de la correspondiente ángulo de sine de. Lo mismo…
Una tabla rápida para las tres funciones trigonométricas recíprocas Usted sabe que las funciones recíprocas tienen valores que son recíprocos, o voltea, de los valores de sus respectivas funciones. El recíproco de seno es cosecante, por lo que cada valor de la función para la cosecante es el recíproco del seno…
Identidades pitagóricas básicos para funciones trigonométricas Las identidades pitagóricas son bloques de construcción para muchas de las manipulaciones de ecuaciones y expresiones trigonométricas. Proporcionan un mayor número de métodos para resolver problemas trigonométricos de manera más eficiente, ya…
Cotangente y cosecante identidades en un círculo unitario A partir de la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, puede derivar cotangente y cosecante identidades pitagóricas. Todo lo que hacemos es tirar un poco de álgebra y aplicar las identidades recíprocas y de relación y -…
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
Encuentra identidades relación trigonometría Trig tiene dos identidades llamados identidades de relación. Esta etiqueta puede ser confuso, ya que todas las funciones trigonométricas se definen por relaciones. En algún momento, sin embargo, los matemáticos pensaron que esta descripción era…
¿Cómo encontrar la inversa de una función trigonométrica Utilice las funciones trigonométricas inversas para resolver ecuaciones como pecado X = 1/2, sec X = -2, O moreno 2X = 1. En las ecuaciones típicas de álgebra, puede resolver por el valor de X dividiendo cada lado de la ecuación por el…
¿Cómo trabajar ambos lados de una identidad trig Con una identidad trigonometría, trabajando en ambos lados de la ecuación es aún más divertido que trabajar en ambos lados de una algebraico ecuación. En álgebra, puede multiplicar cada lado por el mismo número, cuadrado ambos lados, añadir…