Exponentes y radicales en el PSAT / NMSQT

Muchas de las preguntas de álgebra y funciones que te enfrentas en el PSAT / NMSQT contiene exponentes, planteado números o letras. El número o letra no planteado que se llama la base. Cuando los matemáticos hablan de exponentes, los llaman poderes, como en " seis a la octava potencia ".

La segunda potencia se conoce como una cuadrado, y la tercera potencia es una cubo. Si usted tiene un número en la parte frontal de la base, que está llamado coeficiente numéricoyociente. Radicales aparecer aquí y allá en el PSAT / NMSQT. Usted puede conocer a los radicales como raíces cuadradas. Algunos ejemplos:

• La base es 2 y el exponente es 3: 2³ (también llamado dos cubos)

• La base es y y el exponente es 4: y⁴ (lea como y a la cuarta potencia)

• El coeficiente numérico es 5, la base es la, y el exponente es 2: 5la² (lea como cinco al cuadrado)

• La raíz cuadrada de 25 es 5:

  

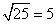
  (¿Por qué 5? Porque 5 x 5 = 25)

El vocabulario no importa, sino lo que haces con la base, exponentes y los coeficientes es importante. Mantenga estas reglas en mente cuando estás resolviendo un PSAT / NMSQT problema con exponentes o radicales:

• Una base con un exponente de cero es igual a 1. Otra forma, más habitual de expresar esto es de base a la potencia cero. Así que 6⁰ = 1, como lo hace X⁰.

• Una base con un exponente de 1 es igual a la base. La mayor parte del tiempo, el 1 es simplemente se omite, pero en sentido estricto, 7¹ = 7 y X¹ = X.

• Un exponente te dice cuántas veces se multiplica la base. Por lo tanto, una base a la segunda potencia es la base multiplicado por sí mismo. (La segunda fuente es mejor conocido como al cuadrado.) Así que 5² = 5 x 5 = 25. Cambiando de tema, 5⁴ = 5 x 5 x 5 x 5 = 625.

• Cuando usted está encontrando una raíz cuadrada, mirar el número bajo el radical y decidir lo que se multiplica por sí mismo para llegar a ese número. Si ve el siguiente, usted sabe que 7 x 7 = 49, por lo que 7 es la raíz cuadrada de 49:

  

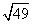
  El exponente te dice cuántas veces hay que multiplicar la base por sí mismo, pero el exponente no es lo que se multiplica. Si ves 4³, multiplicas 4 x 4 x 4 para obtener 64. Usted ¿no multiplicar 4 x 3 para obtener 12.

• Exponentes pueden ser números o fracciones negativas. Un exponente negativo voltea la base mediante la creación de una recíproca, 1 sobre la base. Así X^-3 es el recíproco de X³, que se puede escribir como

  

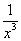
  En exponentes fraccionarios, el denominador de la fracción que le dice que la raíz o radical de aplicar a la base. Así

  

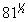
  está pidiendo la raíz cuadrada de 81 ó 9. Otro ejemplo:

  

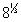
  es 2 porque usted está encontrando la raíz cúbica de 8.

  La calculadora es un buen amigo cuando estás trabajando con poderes. Utilice la y^X botón o el botón ^. Sólo tienes que escribir la base, entonces el exponente, a continuación, el botón de igual signo y ya está! La mayoría de las calculadoras también pueden manejar potencias fraccionarias. Introduzca ^ antes de la fracción, y luego entrar en la fracción.

  Asegúrese de colocar la fracción entre paréntesis! Si olvida el paréntesis, se obtiene la respuesta equivocada. En algunas calculadoras, pulsa la segunda tecla de función para encontrar una raíz en esta forma:

  

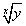
• Para multiplicar como bases, añadir los exponentes. Para dividir como bases, restar los exponentes. Así y⁵ X y⁴ = y⁹ y y⁵ # 247- y² = y³.

  Ni siquiera pensar sobre la aplicación de la regla anterior a bases de diferencia. Nope. Nunca. ¡No va a pasar! Usted tiene un factor hacia fuera o tratar con él como es.

• Para un exponente dentro y fuera de un paréntesis, se multiplican los exponentes. Por lo tanto (5³)² = 5⁶ y (7^X)⁵= 7^5X.

• Para agregar o restar, tanto las bases y los exponentes deben coincidir. No se puede agregar 6² y 8³, ni se puede restar 2X⁴ desde 4X³. Sin embargo, se puede tratar con la suma y la resta, si las bases y los poderes coinciden. Cuando todo coincide, todo lo que tienes que hacer es sumar o restar los coeficientes (los números en frente de la base).

  Aquí hay un problema legal y la solución: 2X² + 5X² = 7X². Un ejemplo más, esta vez con la resta: 9y³ - y³ = 8y³. ¿Te diste cuenta de que 1 se restará de 9, a pesar de que hay 1 aparece en la pregunta? El 1 en frente de la y³ se entiende porque 1 de nada es en sí mismo.

Poder para el pueblo! Ahora que su cabeza está llena de reglas de los exponentes, tratar estos problemas.

1. Simplificar: (X²)³X³

   (LA)X³(B)X⁸(C)X⁹(D)X¹²(E)X¹⁸

2. La expresión 2^la3^la puede escribirse como

   (A) 5^la(B) 5^2la(C) 6^la(D) 6^2la(E) 6^la2

3. Simplificar:

   

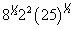
   (A) 5(B) 40

   

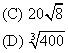
   (E) 400

Ahora compruebe sus respuestas:

1. C. X⁹

   PEMDAS al rescate una vez más! Primero quiere cubicar X², para que pueda obtener X⁶X³, y luego agregar los exponentes juntos ahora que tiene la misma base: X⁹, o La opción (C).

2. C. 6^la

   En este caso usted tiene la copias de 2 y la copias de 3, así que usted puede pensar en cada copia de 2 a juego con una copia de 3 y multiplicando para hacer 6. Se termina con la copias de 6 u opción (C).

3. B. 40

   Tome cada término por sí mismo, simplificar, y luego multiplicar todo junto. En primer lugar,

   

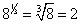
   A continuación, 2² = 4, no hay problema. Finalmente,

   

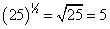
   Ahora, sólo multiplicar los tres resultados juntos: 2 x 4 x 5 = 40. La opción (B) que es!