Dar sentido a exponentes extraños

Los exponentes son una manera rápida para representar la multiplicación repetida. Criar a un base

número a la potencia de un exponente significa multiplicando la base por sí mismo el número de veces indicado por el exponente. Por ejemplo:

10² = 10 x 10 = 1002⁵ = 2 x 2 x 2 x 2 x 2 = 32999¹ = 999

Esta definición tiene sentido cuando el exponente es un entero positivo. ¿Pero qué sucede con un exponente de 0, o un número negativo, o una fracción?

Convertirse en uno con un exponente de 0

Cualquier valor (distinto de cero) elevado a la potencia de 0 es igual a 1. Por ejemplo:

2⁰ = 110⁰ = 11423⁰ = 1

Para entender por qué esta regla funciona, considere los siguientes valores de 2 elevado a la potencia de los primeros números enteros positivos:

21	22	23	24	25	26
2	4	8	16	32	64

Lectura de la segunda fila de la tabla de izquierda a derecha, cada número es el doble del número anterior. Puede seguir este patrón indefinidamente. Del mismo modo, la lectura de la segunda fila de la tabla de derecha a izquierda, cada número es la mitad del número siguiente. Así que usted puede seguir este patrón de la siguiente manera:

20	21	22	23	24	25	26
1	2	4	8	16	32	64

Este tipo de patrón no tiene sólo por una base de 2, pero para todas las bases. Por ejemplo, aquí hay una base del 10:

100	101	102	103	104	105	106
1	10	100	1000	10000	100000	1000000

Por esta razón, cada número (excepto 0) elevado a la potencia de 0 es igual a 1. Para indicar esta regla más formal:

X⁰ = 1 (cuando X # 8800- 0)

Voltear para exponentes negativos

Para entender exponentes enteros negativos, continúe la mesa para una base de 2 para algunas columnas más a la izquierda:

2-4	2-3	2-2	2-1	20	21	22	23	24	25	26
1/16	1/8	1.4	2.1	1	2	4	8	16	32	64

Como se puede ver, el patrón todavía tiene - cada número en la fila inferior es la mitad del número a su izquierda y el doble a su derecha. Observe que cada exponente negativo de un número es el recíproco de la exponente positivo correspondiente. Por ejemplo:

2¹ = 2

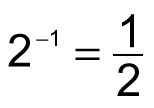
2² = 4

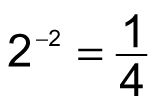
2³ = 8

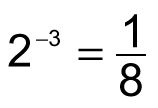
Por esta razón, cada número elevado a un entero negativo es igual a la recíproca de ese número elevado a el valor positivo (absoluto), de dicho número entero. Para indicar esta regla más formal:

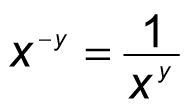
(cuando X # 8800- 0)

El enraizamiento de alrededor de exponentes fraccionarios

Las reglas discutidas anteriormente esquema cómo interpretar cualquier exponente entero. Cuando un exponente es una fracción, es necesario un enfoque diferente.

Para empezar, recuerde que para multiplicar dos valores exponenciales con la misma base, la regla es sumar los exponentes. Por ejemplo:

2³ 2 x⁴ = 2⁷ = 128

Aquí está la regla más general declaró:

(X^la) (X^b) = X^la+b

Esta regla también se aplica a las fracciones, por lo que:

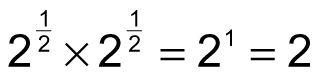
Por lo tanto,

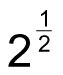
es un valor que, multiplicado por sí mismo, es igual a 2. Esto es:

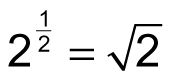
Porque

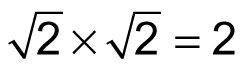
Esta regla funciona para cada base positiva, así que aquí está la regla más general declaró:

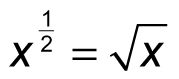
(cuando X # 8805- 0)

Este mismo razonamiento se trabaja para la definición de otras fracciones con 1 en el numerador. Por ejemplo:

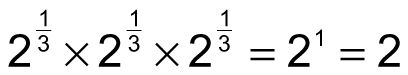
Por lo tanto,

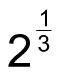
es un valor que, multiplicado por sí mismo 3 veces, es igual a 2. Esto es:

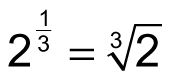
Porque

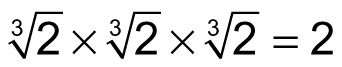
Esta regla también funciona para todas las bases, así que aquí es más general declaró:

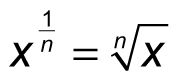
(cuando X # 8805- 0)

Por último, se puede extender este razonamiento a todas las fracciones. Por ejemplo:

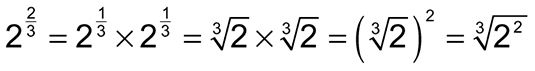
Puede indicar esta regla para todos los números racionales de la siguiente manera:

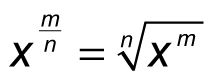
(cuando n # 8800- 0 y X # 8805- 0)