Estrategias para la resolución de ecuaciones acto con variables extra
Algunas ecuaciones en el examen ACT de matemáticas pueden incluir uno o más de más variables. En términos generales, cuando una ecuación tiene más de una variable, no puede resolverlo. Como resultado, en la mayoría de los casos, debe resolver la ecuación en términos de las otras variables - es decir, aislar una variable en un lado de la ecuación.
Ejemplo 1
En la ecuación 2pq + 5qr = 3pr, lo que es el valor de p en términos de q y r?
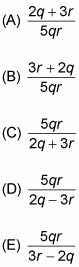
Para responder a esta pregunta, aislar p en un lado de la ecuación. Comience moviendo todo el p de condiciones, a un lado:
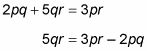
Ahora factorizar p en el lado derecho de la ecuación:
Divide ambos lados por 3r - 2q:
Así que la respuesta correcta es la opción (E).
A veces, cuando una ecuación tiene más de una variable, una variable cae fuera de la ecuación (¡sorpresa!), Lo que le permite resolver para la variable restante. Echa un vistazo a el siguiente ejemplo para ver cómo.
Ejemplo 2
¿Cuál es el valor de X en la ecuación 3 (X + 4y) = 6 (2y + 5)?
(F) 10
(G) 14
(H) 17
(J) 23
(K) No se puede determinar a partir de la información dada
A primera vista, la ecuación no parece solucionable. Pero no se apresure a saltar a esta conclusión. Puede, de hecho, resolver este problema. Comience por distribuir para eliminar los paréntesis:
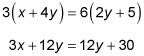
Ahora resta 12y desde ambos lados de la ecuación:
3X = 30
Por arte de magia, la y término ha abandonado, dejándole con una ecuación que se puede resolver fácilmente:
X = 10
La respuesta correcta es la opción (F).
Por último, a veces se puede resolver una ecuación con variables adicionales para una expresión que incluye ambas variables.
Ejemplo 3
Si
lo que es el valor de X - y?
(A) -2
(B) -1
(C) 1
(D) 2
(E) 4
Esta ecuación no puede ser resuelto, ya sea para X o y. Sin embargo, puede aislar la expresión X - y en un lado de la ecuación para responder a la pregunta. Comience multiplicando ambos lados por y - 1:
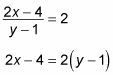
Ahora distribuir en el lado derecho de la ecuación:
2X - 4 = 2y - 2
Aislar el X y y términos de un lado de la ecuación:
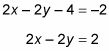
Factorizar un 2 de cada término en el lado izquierdo:
Divide ambos lados por 2:
Así que la respuesta correcta es la opción (C).
-
Cómo asignar valores a las variables en su ti-84 Calculator Plus -
¿Cómo resolver ecuaciones lineales con división -
¿Cómo resolver ecuaciones lineales con dos multiplicación y división -
¿Cómo resolver ecuaciones lineales con la multiplicación -
Resolución de ecuaciones de valor absoluto -
Resolver dos ecuaciones lineales algebraicamente
Los sistemas con tres ecuaciones lineales Cuando se trabaja con sistemas de ecuaciones, puede resolver por una variable a la vez. Así, si una tercera ecuación lineal viene a lo largo (con lo cual, por supuesto, su variable z), Así, tres son multitud. Sin embargo, se puede tratar…
Los fundamentos de la resolución de ecuaciones de álgebra i Uno de los objetivos más comunes en álgebra I es resolver una ecuación. Resolver una ecuación significa para identificar el número o números que puede reemplazar la variable con hacer una declaración verdadera. Usted encontrará el factoring…
Sistemas de ecuaciones de álgebra Resolver En la mayoría de los casos, una ecuación algebraica es resoluble sólo cuando un valor es desconocido - es decir, cuando la ecuación tiene una sola variable. En casos raros, puede resolver una ecuación con dos o más variables debido a una…
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
¿Cómo resolver una ecuación exponencial tomando el logaritmo de ambos lados A veces usted no puede expresar ambos lados de una ecuación exponencial como potencias de la misma base. Al hacer frente a ese problema, puede hacer que el exponente se vaya tomando el logaritmo de ambos lados. Por ejemplo, supongamos que se le…
¿Cómo resolver ecuaciones logarítmicas Ecuaciones logarítmicas toman diferentes formas. Como resultado de ello, antes de resolver ecuaciones que contienen los registros, es necesario estar familiarizado con los siguientes cuatro tipos de ecuaciones de registro:Tipo 1. En este tipo, la…
Resolución de ecuaciones diferenciales separables Ecuaciones diferenciales vuelven más difíciles de resolver el más enredado se vuelven. En ciertos casos, sin embargo, una ecuación que se ve enredado en realidad es fácil de separar. Las ecuaciones de este tipo se llaman ecuaciones separables…
Preparación ASVAB: examen de álgebra Usted se encontrará con problemas de álgebra en el ASVAB. Problemas de álgebra son ecuaciones, lo que significa que las cantidades a ambos lados del signo igual son iguales - son la misma: 2 = 2, 1 + 1 = 2, y 3 - 1 = 2. En todos estos casos, las…
Preparación ASVAB: expresiones matemáticas y ecuaciones El ASVAB se esperan que usted tenga un asimiento firme en ciertas expresiones y ecuaciones matemáticas. Matemáticas y sin expresiones y ecuaciones es como una boca de incendios sin perro- que sólo van de la mano. Entonces, ¿cuál es la…
Militar aptitud de vuelo: operaciones matemáticas para resolver para x La Prueba de Aptitud Vuelo militar podría hacer preguntas que involucran el uso de operaciones matemáticas o expresiones algebraicas. Un expresión algebraica es una colección de números y variables. Usted puede resolver expresiones algebraicas…
Preparación núcleo Praxis: cómo resolver para x y otras variables Tendrá que ser capaz de resolver para x (o cualquier variable) en el examen Praxis Core. Resolución de ecuaciones es una parte enorme de álgebra. La comprensión de cómo hacerlo te pone en una excelente posición para conquistar Praxis Core…
Praxis preparación central: sistemas de ecuaciones El examen de álgebra Praxis Core esperará que usted esté familiarizado con los sistemas de ecuaciones. Ecuaciones con dos variables pueden ser resueltos si van acompañados por una segunda ecuación con al menos una de las variables.Cuando se…