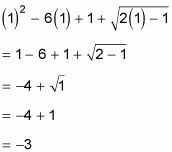Cómo operar en funciones
En su clase de pre-cálculo, se le puede pedir a operar con dos o más funciones. Operar con funciones puede implicar la suma, resta, multiplicación o división.
Adición y sustracción de dos o más funciones
Cuando se le preguntó para agregar funciones, sólo tiene que combinar los términos semejantes, si las funciones tienen ninguna. Por ejemplo, supongamos que tiene tres funciones,
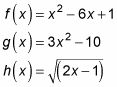
Ahora digamos que (F + g) (X) le está pidiendo que añadir el F(X) y el g(X) Funciones:
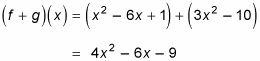
los X2 y 3X2 añadir a 4X2- -6X permanece porque no tiene como términos- 1 y -10 añadir a -9.
Pero ¿qué hacer si se le pide para agregar (g + h) (X)? Usted obtiene la siguiente ecuación:
No tiene términos como para añadir, así que no puedes simplificar la respuesta más lejos. ¡Ya terminaste!
Cuando se le preguntó a restar funciones, usted distribuye el signo negativo a lo largo de la segunda función, usando la propiedad distributiva, y luego tratar el proceso como un problema de suma:
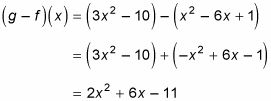
Multiplicando y dividiendo dos o más funciones
Multiplicando y dividiendo funciones es un concepto similar a la suma y resta de ellos. Al multiplicar las funciones, se utiliza la propiedad distributiva y otra y luego añadir los términos como para simplificar. La división de funciones es más complicado, sin embargo.
Vas a abordar la multiplicación primero y guardar la división embaucador para el final. Aquí está la configuración para multiplicar F(X) Y g(X):
(fg) (X) = (X2 - 6X + 1) (3X2 - 10)
Siga estos pasos para multiplicar estas funciones:
Distribuir cada término del polinomio de la izquierda para cada término del polinomio de la derecha.
Se empieza con X2(3X2) + X2(-10) + -6X(3X2) + -6X(-10) + 1 (3X2) + 1 (-10).
Se termina con 3X4 - 10X2 - 18X3 + 60X + 3X2 - 10.
Combine los términos semejantes para obtener la respuesta final a la multiplicación.
Este simple paso le da 3X4 - 18X3 - 7X2 + 60X - 10.
Las operaciones que requieren la división de funciones pueden implicar factoring para cancelar los términos y simplificar la fracción. Si se le pregunta a dividir g(X) Por F(X), Sin embargo, se escribe la siguiente ecuación:
Porque ni el denominador ni el factor de numerador, la nueva función, combinada se simplifica y ya está.
Se le puede pedir que encontrar un valor específico de una función combinada. Por ejemplo, (F + h) (1) le pide que ponga el valor de 1 en la función combinada
Cuando se conecta en 1, se obtiene
Cómo aplicar las operaciones básicas de matrices Al aplicar las operaciones básicas de matrices, funciona muy parecido a operar en múltiples términos dentro parentheses- sólo hay más términos en los "paréntesis" para trabajar. Al igual que con las operaciones sobre los números, un cierto…
Cómo romper una composición de funciones LA composición de funciones es una función que actúa sobre otra. Piense en ello como poniendo una función dentro de la otra - F(g(X)), Por ejemplo, significa que se conecta el todo g(XFunción) en para todos X'pecado F(X). Para resolver este…
¿Cómo encontrar el límite de una función algebraica Cuando su profesor de pre-cálculo le pide que encontrar el límite de una función algebraica, usted tiene cuatro técnicas para elegir: enchufar el X valor, el factoring, racionalizar el numerador, y encontrar el mínimo común denominador.El…
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
¿Cómo simplificar una expresión utilizando identidades recíprocas Cuando se le pregunta para simplificar una expresión que implica cosecante, secante o cotangente, cambia la expresión de funciones que implican seno, coseno, tangente o, respectivamente. Al cambiar las funciones de esta manera, usted está…
Cómo simplificar expresiones trigonométricas con un binomio en el denominador de una fracción Cuando una expresión trigonométrica es una fracción con un binomio en su denominador, siempre tenga en cuenta multiplicando por el conjugado antes de hacer cualquier otra cosa. La mayoría de las veces, esta técnica permite simplificar.Por…
Cómo utilizar las leyes de límite en el cálculo Si conoces las leyes de límite en el cálculo, podrás encontrar los límites de todas las funciones de locos que tu profesor de pre-cálculo puede lanzar su camino. Gracias a limitar las leyes, por ejemplo, usted puede encontrar el límite de…
Sine Express en términos de coseno A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
Sine Express en términos de secante o cosecante A pesar de que cada función trigonométrica es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener algunos…
Sine Express en términos de cotangente A pesar de que cada función de la trigonometría es perfectamente maravilloso, poder expresar cada función trig en términos de una de las otras cinco funciones trigonométricas es con frecuencia a su ventaja. Por ejemplo, usted puede tener…
La identificación de propiedades algebraicas más utilizados en la resolución de identidades Resolución de identidades es casi un rito de paso para los que estudian trigonometría. Hacer frente a la perspectiva de la resolución de identidades - y más tarde simplificar expresiones trigonométricas en cálculo - va mucho más suavemente si…
Preparación ASVAB: examen de álgebra Usted se encontrará con problemas de álgebra en el ASVAB. Problemas de álgebra son ecuaciones, lo que significa que las cantidades a ambos lados del signo igual son iguales - son la misma: 2 = 2, 1 + 1 = 2, y 3 - 1 = 2. En todos estos casos, las…