Cómo núcleo común matemática define las líneas y ángulos
En Common Core matemáticas, los estudiantes de cuarto grado comienzan a ampliar su punto de vista de la geometría más allá de las formas. Piensan en líneas, ángulos y las relaciones que puedan tener con los demás.
Esta actividad genera todo un vocabulario poco más. Por ejemplo, los alumnos estudian líneas paralelas, que son dos líneas en un plano que no se cruzan. Los estudiantes pensar en líneas paralelas como Nunca la reunión, o tal vez como encabezado de la misma extremacción.
Los estudiantes comienzan a hacer distinciones entre líneas (que se extienden infinitamente en cualquier dirección), rayos (que se extiende infinitamente en una sola dirección), y segmentos de línea (que tienen longitud finita y dos puntos finales). Los estudiantes deben investigar si la definición de líneas paralelas se aplica a segmentos de línea. Mira la siguiente figura.
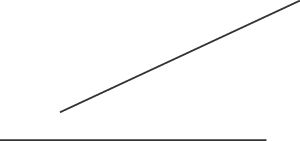
Como muestra la figura, esta definición no se aplica - segmentos de línea pueden no satisfacer, incluso si no son paralelas - lo que se requiere una definición ligeramente diferente. Se puede decir que dos segmentos de recta son paralelos si nunca cumplir, incluso si se extiende infinitamente.
Los estudiantes usan las relaciones de línea y ángulos tales como líneas paralelas y perpendiculares (paralelo líneas están en el mismo plano que el uno al otro, ejecute en la misma dirección, y nunca se encuentran, incluso si se extiende infinitely- Educación físicarperpendicular líneas se encuentran en ángulo recto), y la derecha y los ángulos agudos (a derecho ángulo tiene una medida de 90 grados- una agudo ángulo tiene una medida mayor que 0 grados, pero menos de 90 grados) para clasificar y relacionar formas entre sí.
Por último, los estudiantes reconocen líneas de simetría en formas. Si una forma se dibuja en una hoja de papel, doblando el papel a lo largo del línea de symmetría hace que las dos mitades de la forma para que coincida con la perfección. Un cuadrado tiene cuatro ejes de simetría. Un no # rectángulo 8.208 cuadrados tiene sólo dos líneas de simetría, como se puede ver en esta figura.
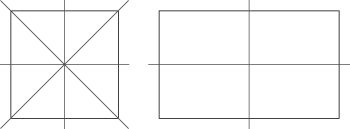
Aunque se pueden conectar las esquinas de un rectángulo y obtener dos mitades iguales # 8208 de tamaño, plegado a lo largo de esta línea no hará que las dos mitades coinciden.
-
Cómo determinar si dos líneas son paralelas o perpendiculares -
Cómo rotación ángulos se miden en la geometría núcleo común -
Formas de partición utilizando conjuntos en matemáticas núcleo común - Matemáticas temas a estudiar para el molinero analogías de prueba (mat)
-
Geometría plana: puntos, líneas, ángulos y formas -
La aplicación de los teoremas transversales
Definiciones y teoremas de líneas paralelas Las líneas paralelas son importantes cuando se estudia cuadriláteros porque seis de los siete tipos de cuadriláteros (todos ellos, excepto la cometa) contienen líneas paralelas. Los ocho ángulos formados por líneas paralelas y una transversal…
Conocer las líneas Hay diferentes tipos de líneas (o segmentos o rayos) o pares de líneas (o segmentos o rayos). Puede identificar líneas individuales en base a la dirección que están apuntando (horizontal, vertical, o ninguno), y se puede categorizar pares de…
¿Cómo demostrar que un cuadrilátero es un rectángulo Hay tres maneras de demostrar que un cuadrilátero es un rectángulo. Tenga en cuenta que los métodos segundo y tercero requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos los ángulos de…
Trabajando con más de una transversal Cuando un dibujo de líneas paralelas-with-transversal contiene más de tres líneas, la identificación de ángulos congruentes y complementarias puede ser un poco difícil. La siguiente figura muestra dos líneas paralelas con dos transversales.Si…
Cifras trigonométricas básicas Segmentos, rayos y líneas son algunas de las formas básicas que se encuentran en la geometría, y son casi tan importantes en trigonometría. Utiliza esos segmentos, rayos y líneas para formar ángulos.Dibujo segmentos, rayos y líneasLA segmento…
Ángulos trigonométricos básicos Cuando dos líneas, segmentos, o rayos táctil o se cruzan entre sí, forman un ángulo o ángulos. En el caso de dos líneas que se cruzan, el resultado es cuatro ángulos diferentes. Cuando dos segmentos se cruzan, pueden formar uno, dos, o cuatro…
Cómo reconocer las líneas paralelas y perpendiculares Dos líneas son paralelo si tienen la misma pendiente. Dos líneas son perpendicular si sus pendientes son recíprocos negativos de unos a otros. Los números que están recíprocos negativos tener un producto -1.Considere las siguientes laderas de…
Encontrar la fuerza de la gravedad a lo largo de un plano inclinado Puede usar la física para determinar la fuerza de la gravedad sobre un objeto que se mueve a lo largo de un plano inclinado. Puede romper el peso del objeto en componentes que son paralelas a y perpendicular al plano. El componente perpendicular al…
La teoría de cuerdas y la historia de la geometría no euclidiana Antes de la teoría de cuerdas introdujo el concepto de dimensiones extra, la fascinación por la extraña deformación del espacio en la década de 1800 fue tal vez la nada tan claro como en la creación de la geometría no euclidiana, donde los…
Preparación ASVAB: revisión de geometría Usted tendrá que tener un conocimiento básico de la geometría para el ASVAB. Geometry es ". La rama de las matemáticas que se ocupa de la deducción de las propiedades, la medición, y las relaciones de puntos, líneas, ángulos y figuras en el…
Saber ángulos, líneas y transversales relacionados LA transversal es una línea que se cruza al menos otras dos líneas en un punto diferente para cada uno. Esta situación implica múltiples ángulos y relaciones angulares.La transversal en el diagrama es la línea que va hacia abajo y hacia la…
Cómo resolver problemas de ángulo en el PSAT / NMSQT Cuando dos líneas se encuentran forman un ángulo. Los ángulos se miden en grados. En el PSAT / NMSQT, usted no encontrará ningún ángulos negativos o cero, y probablemente no tendrá que lidiar con los ángulos fraccionarios o bien (sin 45,9…