Cómo utilizar los intervalos de confianza para proporciones en seis sigma
A veces, en un proyecto Seis Sigma, se le enfrenta con intervalos de confianza y proporciones. Al calcular el número de éxitos de un cierto número de intentos - como " cuatro de cada cinco dentistas recomiendan chicles sin azúcar " - Usted puede escribir esta proporción (p) Matemáticamente como
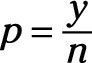
dónde y es el número de éxitos y n es el número total de intentos o ensayos.
Cálculo de un porcentaje crea una nueva distribución de muestreo. El intervalo de confianza resultante en torno a una proporción calculada es
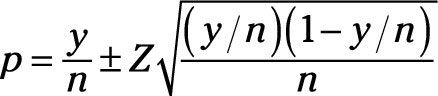
Así, como ejemplo, si querías ser de 90 por ciento seguro de la proporción calculada para las cuatro de cada cinco dentistas, sería calcular el intervalo de confianza de la siguiente manera:
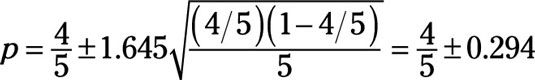
Este resultado significa que, con 90 por ciento de confianza, la proporción de cuatro de cada cinco dentistas realmente podría ser tan pequeño como un medio o tan grande como una sola.
En realidad, las proporciones no puede ser nunca menor que cero o mayor que uno. Así que si su intervalo de confianza para la proporción excede estos límites naturales, simplemente ajustar el intervalo de confianza para el límite natural.
Si usted está comparando la diferencia entre dos proporciones, tales como
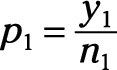
y
el intervalo de confianza para esta diferencia se hace
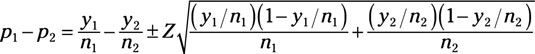
Para ilustrar este intervalo de confianza, imagina que eres parte de una empresa con dos líneas de producción. Usted sospecha que su Toledo (T) planta produce una mayor proporción de buenos artículos (rendimiento) que tu Buffalo (B) planta.
Usted selecciona muestras de tamaño nT = nB = 300 de cada planta y encontrar que el número de buenos artículos de la planta de Toledo (yT) Es 213, mientras que el número de la planta de Buffalo (yB) Es 189. Eso significa que un intervalo de confianza del 95 por ciento para la diferencia entre el Toledo y los rendimientos Buffalo es
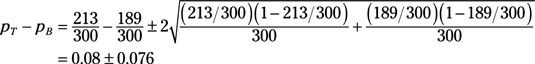
o, equivalentemente, [0.004, 0.156]. Debido a que este intervalo de confianza no incluye cero, se puede concluir - con un 95 por ciento de confianza - que la planta de Toledo produce, en promedio, una mayor proporción de buenos elementos que la planta de Buffalo.
-
Cómo probar proporciones de datos con r - Comprobación de confianza valores críticos de intervalos estadísticos
-
Comprobación de fórmulas para los intervalos de confianza - La elección de un nivel de confianza de una muestra de población
-
Los intervalos de confianza y las proporciones de población -
Definición y cálculo de margen de error
Sacar conclusiones sobre una población con intervalos de confianza y pruebas de hipótesis Al sacar conclusiones sobre una población a partir de muestras elegidas al azar (un proceso llamado inferencia estadística), Puede utilizar dos métodos: intervalos de confianza y pruebas de hipótesis.Intervalos de confianzaLA intervalo de…
Cómo determinar el intervalo de confianza para una proporción de la población Usted puede encontrar el intervalo de confianza (IC) para una proporción de la población para mostrar la probabilidad estadística de que es probable que se produzcan dentro de la población de una característica.Cuando una característica que se…
Cómo estimar la diferencia entre dos proporciones Para estimar la diferencia entre dos proporciones de población con un intervalo de confianza, puede utilizar el teorema del límite central, cuando los tamaños de las muestras son lo suficientemente grandes (por lo general, cada uno por lo menos…
¿Cómo encontrar t *-valores para los intervalos de confianza Intervalos de confianza estimación de los parámetros de población, tales como la media poblacional, mediante el uso de una estadística (por ejemplo, la media de la muestra) más o menos un margen de error. Para calcular el margen de error para…
En cuanto a los valores críticos del intervalo de confianza Los valores críticos (z*-valores) son un componente importante de los intervalos de confianza (la técnica estadística para estimar parámetros poblacionales). los z* -valor, que aparece en el margen de la fórmula de error, mide el número de…
Topografía intervalos de confianza estadísticos En estadística, un intervalo de confianza es una conjetura acerca de algunas características de la población. Un intervalo de confianza contiene un plus estimación o menos un inicial margen de error (la cantidad que usted espera que sus…
Fundamentos del intervalo de confianza En bioestadística, es importante estar cómodo con los conceptos básicos y la terminología relacionadas con intervalos de confianza. Esta es un área donde los matices de significado puede ser complicado, y el derecho; palabras que suenan se…
El intervalo de confianza en torno a una media Del mismo modo que la SE fórmulas (error estándar) dependen de qué tipo de estadística de la muestra que está tratando con (ya sea que estés medir o contar algo o conseguir que a partir de un programa de regresión o de algún otro cálculo),…
El intervalo de confianza en torno a una proporción Si se va a encuestar a 100 niños típicos y encontrar que 70 de ellos como el chocolate, que le estimar que el 70 por ciento de los niños como el chocolate. ¿Cuál es el intervalo de confianza del 95 por ciento (CI) en torno a que la estimación…
El intervalo de confianza alrededor de un coeficiente de regresión Este es un momento en que no es necesario ningún fórmulas porque usted no debe tratar de calcular los errores estándar o los intervalos de confianza (IC) de los coeficientes de regresión a ti mismo. Cualquier programa de regresión buena puede…
Cómo usar intervalos de confianza para verificar las diferencias entre los resultados Los intervalos de confianza le dan una forma de cuantificar el grado de variación aparecerá en mediciones repetidas y cálculos estadísticos para Six Sigma. Saber cómo crear intervalos de confianza, podrás decirle a su jefe, " Con el 99,7 por…
Cómo utilizar los intervalos de confianza para seis sigma Debido a que las muestras son accesibles, las muestras y los intervalos de confianza son la herramienta primaria de datos para la comprensión de un negocio o el procesamiento de seis situaciones de rendimiento Sigma. Pero las muestras nunca se le…