Cómo utilizar los intervalos de confianza para seis sigma

Debido a que las muestras son accesibles, las muestras y los intervalos de confianza son la herramienta primaria de datos para la comprensión de un negocio o el procesamiento de seis situaciones de rendimiento Sigma. Pero las muestras nunca se le puede dar una medida exacta de lo que está pasando en la población subyacente. Son intrínsecamente borrosa! ¿Qué tan seguro puede ser que su muestra lo suficientemente precisa refleja lo que realmente está sucediendo en la población subyacente?

La clave para la toma de decisiones objetivo radica en intervalos de confianza. Ellos usan el teorema del límite central para cuantificar cuánta confianza puede colocar en cualquiera de sus medidas o conclusiones estadísticas de muestras.

La confianza de medición hablamos aquí no se refiere a la capacidad de su sistema de adquisición de mediciones. En su lugar, la confianza de medición asume que tiene un sistema perfecto, ideal para la adquisición de sus medidas. Este escenario debe servir como un recordatorio de la importancia de la validación de la capacidad de su sistema de medición es.

Por ejemplo, supongamos que su habitante ha producido 5.000 bolígrafos. ¿Quieres saber el diámetro medio de esta población, por lo que se selecciona al azar 30 plumas de la población, mida cada uno de sus diámetros, y calcular la media para ser 0.120 pulgadas.

De pronto, su jefe se precipita en su oficina y le pregunta: " Cuál es el diámetro medio de nuestras últimas plumas? Nuestro cliente acaba de llamar y dijo que rechazará todo el lote si el promedio es superior a 0,125 pulgadas "! Su jefe espera ansiosamente su respuesta. ¿Qué estás diciendo? ¿Qué tan seguro está usted en su promedio calculado?

El teorema del límite central dice que si se repite la medición de 30 muestras, que obtendrá un promedio ligeramente diferente. Su cliente, también, al comprobar su propia muestra. Pero lo diferente que será cada cálculo de la media de ser? Los intervalos de confianza le dan una forma de cuantificar el grado de variación aparecerá en mediciones repetidas y cálculos estadísticos.

Saber cómo crear intervalos de confianza, podrás decirle a su jefe, " Con el 99,7 por ciento de certeza, nuestra diámetro medio de la pluma será dentro de los requerimientos de nuestro cliente ".

Usted ve las medias todos los días. Desafortunadamente, muy pocos de ellos se comunican con un intervalo de confianza.

Cómo tomar decisiones con grandes muestras

Cuando su tamaño de la muestra cuenta con más de 30 puntos de datos, se puede calcular la confianza en torno a la media real de la población (# 956-) como

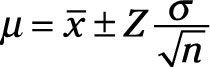
dónde

• Z es el valor de sigma correspondiente al nivel deseado de confianza que usted desea tener.

• # 963- es la desviación estándar calculada a partir de su muestra.

• n es el número de puntos de datos en su muestra.

  

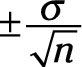
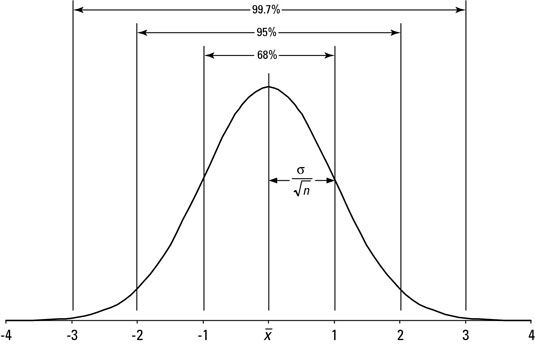
de la media de la población real. Además, el 95 por ciento de [neq16006] s calculados están dentro

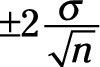
de la media de la población real. Y el 99,7 por ciento de [neq16008] s calculados están dentro

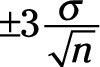
de la media de la población real. Esta fórmula funciona cada vez que tenga más de 30 medidas en su muestra.

Tomar decisiones con muestras pequeñas

Cuando usted tiene sólo unos pocos puntos de datos en la muestra, usted no es capaz de obtener una estimación precisa de la desviación estándar de la población # 963-. Con estas pequeñas muestras, los estadísticos reemplazar la variable # 963- con s para comunicar que es suficiente con una estimación inexacta de la desviación estándar de población de la muestra.

Así que cuando su muestra tiene entre 2 y 30 puntos de datos, usted tiene que utilizar un factor diferente en lugar de Z. Los estadísticos llaman a este nuevo factor de muestras de pequeño tamaño t. t es más conservador debido a que su tamaño de muestra más pequeño disminuye la precisión de su valor calculado para la desviación estándar. Para cada nivel de confianza deseado, t se ajusta dependiendo del número de puntos de datos están en su muestra.

Usando t, la fórmula para el intervalo de confianza en torno a la media de la población se convierte en verdadera

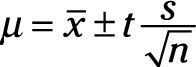
donde el valor de t depende de su nivel deseado de confianza y el número de puntos de datos en su muestra.