Cómo utilizar el teorema del límite central para seis sigma

¿Qué sucede cuando usted toma repitió muestras de la misma población? Esta idea es importante cuando se utiliza el teorema del límite central para Six Sigma. Imagínese lanzar una moneda diez veces y contando el número de cabezas que obtiene. Las leyes de la probabilidad decir que usted tiene una probabilidad de 50-50 de que salga cara en un solo lanzamiento. Si usted lanza la moneda diez veces, lo que espera conseguir cinco cabezas.

Vaya por delante y tire una moneda de su bolsillo y probar este experimento, si quieres. Usted no puede conseguir los esperados cinco cabezas después de voltear la moneda diez veces. Usted puede obtener sólo tres cabezas. O tal vez usted consigue seis. Después de cada repetición experimento (muestra), se contó el número de cabezas de los diez lanzamientos. El experimento se repitió 10, a continuación, 100, y finalmente 1.000 veces.

Este experimento cara o cruz es análogo a cualquier situación donde se toma una muestra de datos de una población - como tomar una muestra de las mediciones de un proceso y el cálculo de la media. Dos hechos importantes se deben a que se puede generalizar a cualquier situación de muestreo:

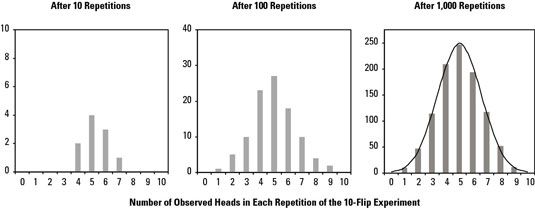
• Las repeticiones del evento de medición producen diferentes resultados de resultado. Es decir, el resultado es variable de una muestra a. En el experimento de la moneda-mueve de un tirón, no cada repetición de la serie de diez flip produjo los esperados cinco cabezas. Lo mismo es cierto si se toma en repetidas ocasiones un promedio de cinco puntos del grosor del papel que sale de una fábrica de papel.

• Esta medición resultante, o distribución muestral, se distribuye normalmente. La variación también se centra en el resultado esperado. Y cuantas más repeticiones que usted hace, la variación de muestreo cada vez más cerca llega a una distribución perfectamente normal.

Los estadísticos llaman repitieron las mediciones de una característica o un proceso muestras. Así que la variación que se produce en los acontecimientos de muestreo repetidas que ellos llaman su distribución muestral.

Las mismas mediciones de muestras no son las únicas cosas que varían cuando usted está tratando con muestras repetidas. Los estadísticos han refinado y perfeccionado definiciones técnicas de lo que se llama la del límite central alorem. Aunque cada definición es igualmente misteriosa, dicen la misma cosa básica: Al calcular las estadísticas en una muestra, repitiendo esos cálculos en otra muestra de la misma población siempre te dará un resultado ligeramente diferente.

Además, la colección de repetidas resultados calculados siempre tendrá una distribución en sí. Esta variación de muestreo sigue una curva de campana normal, centrado en la verdadera variación de la población subyacente. Además, la anchura de la distribución de muestreo depende del número de medidas que usted toma en cada muestra. Cuanto mayor sea el tamaño de la muestra, más estrecha es la variación de muestreo.

Aunque los estadísticos a menudo tienen dificultades para explicar el teorema del límite central, su poder y utilidad son, sin embargo, notable. Los resultados del teorema del límite central le permiten predecir los límites del futuro y para cuantificar los riesgos del pasado.