¿Cómo encontrar la relación de incertidumbre de Heisenberg desde cero
Si usted ha leído a través de los últimos tramos, que está ahora armado con toda esta nueva tecnología: hermitianos y conmutadores. ¿Cómo se puede poner a trabajar? Puede llegar a la relación de incertidumbre de Heisenberg partir prácticamente de cero.
Aquí hay un cálculo que te lleva desde algunas definiciones básicas para la relación de incertidumbre de Heisenberg. Este tipo de cálculo muestra lo fácil que es usar el sujetador y ket notación de base menos que la versión de la matriz completa de los vectores de estado. Este no es el tipo de cálculo que usted tendrá que hacer en clase, pero lo sigue a través - saber utilizar mercados, sostenes, conmutadores, y los operadores hermitianas es vital en los próximos capítulos.
La incertidumbre en una medición del operador hermitiana nombrado se da formalmente por
Eso es,
es igual a la raíz cuadrada del valor de expectativa de A2 menos el valor esperado cuadrado de A. Si usted ha tomado ninguna clase de matemáticas que se ocupan de las estadísticas, esta fórmula puede ser familiar para usted. Del mismo modo, la incertidumbre en una medición usando el operador B es hermitiana
Ahora considere el operadores
(no las incertidumbres
más), y asumir que la aplicación de
ya que los operadores le da valores de medición como éste:
Al igual que cualquier operador, utilizando
puede dar lugar a nuevos mercados:
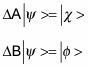
Aquí está la clave: La desigualdad de Schwarz le da
Así se puede ver que el signo de la desigualdad,
que desempeña un papel importante en la relación de incertidumbre de Heisenberg, que ya se ha colado en el cálculo.
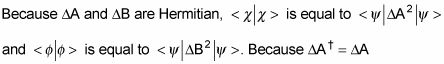
(la definición de un operador hermítica), se puede ver que
Esto significa eso
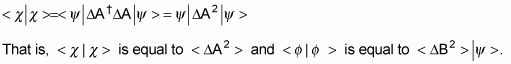
Así que usted puede reescribir la desigualdad de Schwarz así:
Vale, donde ha conseguido esto usted? Es hora de ser inteligente. Tenga en cuenta que usted puede escribir
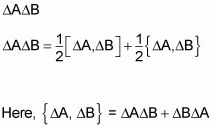
es la anticommutator de los operadores
(las constantes y restar a cabo), se puede reescribir esta ecuación:
Aquí es donde las matemáticas se pone intensa. Echa un vistazo a lo que sabe hasta el momento:
El conmutador de dos operadores hermitianas, [a, b], es anti-hermitiana.El valor esperado de un anti-hermitiana es puramente imaginario.los
es hermitiana.El valor esperado de un hermítica es real.
Todo esto significa que se puede ver el valor esperado de la ecuación como la suma de los bienes
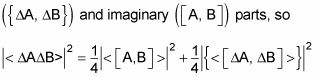
Y debido a que el segundo término de la derecha es positivo o cero, se puede decir que se cumple lo siguiente:
¡Menos mal! Pero ahora comparar esta desigualdad a la relación de la utilización anterior de la desigualdad de Schwarz:
Combinando las dos ecuaciones le da esto:
Esto tiene el aspecto de la relación de incertidumbre de Heisenberg, a excepción de los soportes de valor expectativa molestos, lt; >, Y el hecho de que
aparecerá cuadrado aquí. Usted quiere reproducir la relación de incertidumbre de Heisenberg aquí, que se ve así:
Bien, así que ¿cómo se consigue el lado izquierdo de la ecuación de
Debido a una ecuación anterior le dice que
usted sabe lo siguiente:
Tomando el valor esperado del último término de esta ecuación, se obtiene este resultado:
Cuadrar la ecuación anterior
para obtener lo siguiente:
Y comparando esa ecuación a la que conoce, usted concluye que
Guay. Este resultado significa que
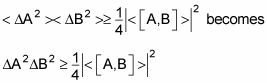
Esta desigualdad en el último significa que
Bien bien bien. Así el producto de dos incertidumbres es mayor que o igual a la mitad del valor absoluto del conmutador de sus respectivos operadores? Guau. ¿Es esa la relación de incertidumbre de Heisenberg? Bueno, eche un vistazo. En la mecánica cuántica, el operador de momento se ve así:
Y el operador para el impulso en la dirección x es
¿Cuál es el conmutador del operador X (que sólo devuelve la X posición de una partícula) y
se obtiene la siguiente desigualdad (recuerde,
aquí están las incertidumbres en X y
no los operadores):
¡Hot dog! Esa es la relación de incertidumbre de Heisenberg. (Observe que derivando desde cero, sin embargo, usted no ha hecho restringido el mundo físico a través del uso de las matemáticas abstractas - que simplemente has demostrado, mediante unos supuestos básicos, que no se puede medir el mundo físico con perfecta exactitud.)



