Cómo estimar y predecir el valor de y en una ecuación de regresión múltiple
Se puede estimar y predecir el valor de Y usando una ecuación de regresión múltiple. Con el análisis de regresión múltiple, la ecuación de regresión población puede contener cualquier número de variables independientes, tales como
En este caso, hay k variables independientes, indexados de 1 a k.
Por ejemplo, supongamos que el departamento de Recursos Humanos de una gran empresa quiere determinar si los sueldos de sus empleados están relacionados con años de los empleados de la experiencia laboral y su nivel de educación de postgrado. Para probar esta idea, el departamento de recursos humanos recoge una muestra de ocho empleados al azar y registra sus salarios anuales (medidos en miles de dólares al año), años de experiencia y años de educación de postgrado.
Las siguientes variables se definen:
Y representa el salario anual de un empleado, medido en miles de dólares.
X1 representa el número de un empleado de años de experiencia de trabajo. Un valor de 0 representa alguien que no tiene experiencia en el trabajo (como un recién graduado de la universidad).
X2 representa el número de años de educación de postgrado. Un valor de 0 representa un graduado de la universidad sin la educación de postgrado.
En la siguiente tabla se muestran los datos de la muestra.
| Y (Sueldo anual, en miles) | X1 (Años de experiencia) | X2 (Años de Graduados de Educación) |
|---|---|---|
| 80 | 1 | 0 |
| 90 | 2 | 1 |
| 100 | 3 | 2 |
| 120 | 4 | 2 |
| 85 | 1 | 0 |
| 95 | 2 | 1 |
| 105 | 2 | 2 |
| 140 | 8 | 3 |
El departamento de recursos humanos se ejecuta una regresión utilizando un programa de hoja de cálculo, como Excel. Esta figura muestra los resultados.
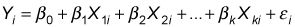
Tomando los coeficientes de intersección y de pendiente (X1 y X2) desde el Coeficientes columna en la figura, se puede llenar en la ecuación de regresión estimada como
(Los valores se han redondeado a dos decimales.)
Esta ecuación muestra que el siguiente es válido para esta empresa:
El salario inicial para un nuevo empleado sin experiencia o de postgrado de educación es $ 76.470. Esta cantidad se basa en la intersección de la ecuación de regresión.
Cada año adicional de experiencia agrega $ 5,320 a SALARIO de un empleado de esta cantidad se basa en el coeficiente de X1 (años de experiencia).
Cada año adicional de educación de postgrado añade $ 7,350 al salario de un empleado, que se basa en el coeficiente de X2 (años de educación de postgrado).
En cada caso, se multiplican los coeficientes de $ 1.000 para obtener el impacto en el salario debido a estas variables se miden en miles de dólares por año.
La intersección de la ecuación, 76.47, muestra el valor de Y (salario anual del empleado) cuando ambas cosas X1 (años de experiencia) y X2 (años de educación de postgrado) son iguales a 0 (es decir, un nuevo empleado sin experiencia o la educación de posgrado). La intersección muestra que el salario inicial es
El coeficiente de X1, 5.32, muestra la cantidad de Y cambios debido a un cambio de una unidad en X1. Porque X1 representa años de experiencia, un cambio de una unidad en X1 es un año más de experiencia. Por lo tanto, cada año adicional de experiencia suma
al salario de un empleado.
El coeficiente de X2, 7.35, muestra la cantidad de Y cambios debido a un cambio de una unidad en X2. Porque X2 representa años de educación de postgrado, un cambio de una unidad en X2 es de un año adicional de estudios de posgrado. Por lo tanto, cada año adicional de estudios de posgrado agrega
al salario de un empleado.
Puede utilizar la ecuación de regresión múltiple para los salarios de los empleados para predecir el salario anual de un empleado con una cantidad específica de experiencia y educación. Por ejemplo, supongamos que un empleado elegido al azar tiene cinco años de experiencia y un año de educación de postgrado. El salario predicho de este empleado es
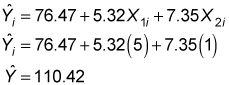
Este resultado muestra que el salario anual previsto es (110,42) ($ 1,000) = $ 110.420.
-
Cómo utilizar regresiones lineales en el análisis predictivo - El análisis de regresión en el análisis estadístico de los datos grande
-
Realice regresiones desde dentro de la aplicación calculadora TI-Nspire -
Los resultados de una regresión en la TI-Nspire -
Econometría y el modelo log-lineal -
La estimación de la función de regresión y de los residuos
Cómo determinar un incremento salarial sobre la base de un porcentaje Si usted necesita para calcular alguien es Incremento salarial o elevar basado en el porcentaje del aumento, usted puede hacer esto mediante la propiedad distributiva. He aquí un ejemplo:El salario de Alison era $ 40.000 el año pasado, y al final…
Estadísticas de las empresas: utilizan el análisis de regresión para determinar la validez de las relaciones El análisis de regresión es una de las técnicas estadísticas más importantes para aplicaciones de negocios. Es una metodología estadística que ayuda a estimar la fuerza y la dirección de la relación entre dos o más variables. El…
¿Cómo las empresas utilizan las estadísticas de análisis de regresión El análisis de regresión es una herramienta estadística utilizada para la investigación de las relaciones entre las variables. Por lo general, el investigador desea saber el efecto causal de una variable sobre otra - el efecto de un aumento de…
Cómo calcular el coeficiente de determinación ajustado Puede utilizar el coeficiente de determinación ajustado para determinar qué tan bien una ecuación de regresión múltiple "encaja" los datos de la muestra. El coeficiente de determinación ajustado está estrechamente relacionado con el…
Cómo estimar una tendencia en un modelo de regresión de series de tiempo Para estimar un modelo de regresión de series de tiempo, una tendencia debe ser estimado. Se empieza por la creación de un gráfico de líneas de las series temporales. El gráfico de líneas muestra cómo una variable cambia con el tiempo- que…
El intervalo de confianza alrededor de un coeficiente de regresión Este es un momento en que no es necesario ningún fórmulas porque usted no debe tratar de calcular los errores estándar o los intervalos de confianza (IC) de los coeficientes de regresión a ti mismo. Cualquier programa de regresión buena puede…
Hablando alrededor de obstáculos de educación en una entrevista de trabajo Si tiene que hacer frente a su falta de educación que se requiere en una entrevista de trabajo, hablar de su experiencia y habilidades como la educación. Mención conocimientos y habilidades basado en la experiencia, por ejemplo, y redirigir la…
La determinación de sueldo neto de los empleados en su negocio Sueldo neto es la cantidad que una persona se paga después de restar los impuestos y beneficios. Así, después de todas las deducciones se restan del salario bruto de un empleado, que se quedan con el salario neto. Después de averiguar todos los…
La determinación de los tipos de sueldos y salarios, cuando la dotación de personal de su empresa Usted tiene mucho margen de maniobra en cuanto al nivel de los salarios y sueldos que paga a sus empleados, pero usted todavía tiene que seguir las reglas establecidas por el Departamento de Trabajo de Estados Unidos. Al decidir sobre los sueldos y…
Cómo calcular la nómina para los empleados en su negocio Al conocer los detalles acerca de descuentos de la retención de sus empleados y sus costos de beneficios, usted puede entonces calcular la nómina final para su negocio y que lo ponga a los libros.Cálculo de la nómina de los empleados por…
Beneficios libres de impuestos para sus empleados La mayoría de los beneficios están exentos de impuestos, o no gravados. Asistencia sanitaria y las prestaciones de jubilación son los más comunes de este tipo de beneficio. De hecho, de accidentes y de salud los beneficios y prestaciones de…
Cómo calcular la regresión lineal múltiple para seis sigma ¿Qué deben hacer los profesionales de Six Sigma ver con todas las situaciones en las que más de un X influye en un Y? Tu usas regresión lineal múltiple. Después de todo, ese tipo de situación es más común de lo que una sola variable que…