Economía de la empresa: cómo ganar juegos infinitamente repetidos

El mundo de los negocios se caracteriza por numerosas decisiones tomadas durante un período prolongado de tiempo. En economía de la empresa, la teoría de juegos ayuda a encontrar la mejor decisión que tomar. Una recompensa se asocia con cada decisión, y los jugadores también tienen la memoria de las decisiones pasadas. Para todos los efectos prácticos, el horizonte de tiempo de negocios es infinita - el juego nunca termina. El resultado es una infinitamente repetida juego.

En los juegos infinitamente repetidos, es necesario tener en cuenta no sólo cómo tu rival juega esta ronda, pero también cómo esta ronda del juego influye en futuras rondas.

Otro factor que debe tener en cuenta en los juegos infinitamente repetidos es el valor temporal del dinero. Un dólar recibido hoy vale más que un dólar recibido dentro de un año, debido a que el dólar recibido hoy pueden ganar intereses. Por lo tanto, los pagos futuros se deben ajustar mediante el cálculo del valor actual.

La estrategia típica usada en un juego infinitamente repetido es la estrategia de gatillo. LA estrategia de gatillo es contingente en el juego pasado - un jugador toma la misma acción hasta que otro jugador toma una acción que desencadena un cambio en la acción del primer jugador.

Un ejemplo de una estrategia de disparo utilizado en juegos que implican un dilema del prisionero es ojo por ojo. Cuando se utiliza un tit-for-tat estrategia, se empieza por asumir jugadores cooperan. En cualquier ronda posterior, usted hace lo que su rival lo hizo en la ronda anterior. Por lo tanto, si su rival, engañó a un entendimiento en la última ronda, haces trampa esta ronda. Si tu rival cooperó en la última ronda, cooperas esta ronda.

Una estrategia de ojo por ojo tiende a conducir a la cooperación porque castiga a los tramposos en la siguiente ronda. Además, se perdona a los tramposos si posteriormente deciden cooperar. Uno de los requisitos de la estrategia de ojo por ojo es que los jugadores son estables. Los jugadores recuerdan cómo se juega el juego en el período anterior. Los nuevos jugadores pueden alterar el equilibrio necesario al no tener la memoria necesaria del comportamiento pasado.

En este ejemplo, hay dos ferrocarriles puede reconocer desde el juego de mesa Monopoly - el ferrocarril de Pennsylvania y de la B O Railroad. Aquí, están compitiendo por el tráfico entre las mismas ciudades. Los ferrocarriles pueden o engañar a otros y cobrar precios más bajos para la carga, o pueden cooperar y cobrar precios más altos. La ilustración muestra la tabla de ganancias como resultado de las ganancias anuales.

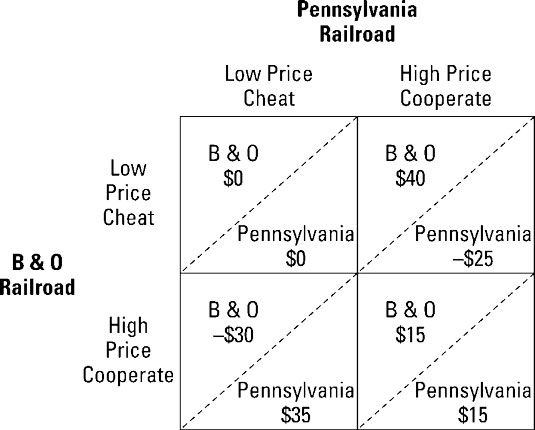
En este cuadro de ganancias, ambos ferrocarriles tienen una acción dominante - a cobrar un precio bajo. Como resultado, ambos ganan $ 0. Este resultado es aún el dilema de otro preso.

Si estos ferrocarriles juegan el juego mucho tiempo, ambos reconocen que la cooperación mediante el cobro de un precio muy alto permite que tanto para ganar cada año $ 15 millones. Hacer trampa mediante el cobro de un precio bajo puede conducir a una gran recompensa de un año, pero el costo asociado con tener su truco rival en el próximo año es muy alta. Considere lo que sucede en una estrategia de ojo por ojo:

1. Si el B O Railroad cobra un alto precio, y el ferrocarril de Pennsylvania engaña y cobra un precio bajo, B Las pérdidas de S son $ 30 millones y ganancias de Pennsylvania es de $ 35 millones.

2. Siguiendo una estrategia de ojo por ojo, el B O Railroad cobra un precio bajo del próximo año, y el ferrocarril de Pennsylvania sigue cobrar un precio bajo.

   Los ferrocarriles están encerrados en una situación de beneficio cero para siempre, porque la B O Railroad mantenga la aplicación del precio bajo que el ferrocarril de Pennsylvania cobrará el año anterior. Los ferrocarriles están en un dilema del prisionero.

3. Siguiendo una estrategia de ojo por ojo, el B O cobra un precio bajo del año que viene y el ferrocarril de Pennsylvania cobra un alto precio.

   El B O Railroad gana $ 40 millones en ganancias y Pennsylvania pierde $ 25 millones. Pero ahora el juego se puede volver a la cooperación. El B O perdona el ferrocarril de Pennsylvania para hacer trampa en la primera ronda y en las rondas futuras, cada ferrocarril gana $ 15 millones.

En cierto sentido, el ferrocarril de Pennsylvania tiene que aceptar el castigo por hacer trampa en el primer lugar. Pero aceptar que el castigo un año lleva a una situación en la que ambos ferrocarriles vuelvan a $ 15 millones de beneficio anual. Si los ferrocarriles siguen engañar mediante el cobro de un precio bajo, cada uno reconocerá que la cooperación no paga, y serán para siempre encerrado en cobrar un precio bajo y recibir beneficio cero.

En este juego infinito, ambos ferrocarriles hacen más beneficios si cooperan todo el tiempo y nunca caen en una estrategia de ojo por ojo.

Si usted tiene un horizonte de tiempo infinito, el valor presente de un flujo constante de futuros ingresos netos iguales

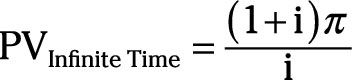
dónde # 240- es el ingreso neto ganado cada año y yo es la tasa de interés.

En el ejemplo anterior, si el B Ferrocarriles S y Pennsylvania cooperan, cada uno de ellos ganan $ 15 millones de beneficio anual. Si el B O Railroad tiene un horizonte de tiempo infinito, el valor actual de $ 15 millones beneficio anual a una tasa de interés del 5 por ciento es

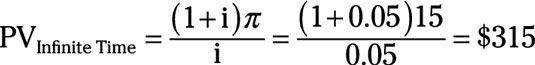
o $ 315 millones.