¿Cómo transformar horizontalmente una función
Usted puede transformar cualquier función en una función relacionada desplazando horizontalmente o verticalmente, darle la vuelta (reflejándola) horizontal o verticalmente, o estirando o encogiendo horizontal o verticalmente. Vamos a través de las transformaciones horizontales. Considere la función exponencial
Echa un vistazo a la siguiente gráfica.
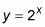
Realiza cambios horizontales mediante la adición de un número para o restando un número de la variable de entrada X, o multiplicando X por algún número.
Todas las transformaciones horizontales, excepto reflexión, funcionan de la opuesto manera que se espera:
Agregando a X hace la función de ir a la izquierda.
Restando de X hace la función de ir a la derecha.
Multiplicando X por un número mayor que 1 se contrae la función.
Multiplicando X por un número menor que 1 se expande la función.
Traducción Horizontal
Por ejemplo, la gráfica de y = 2X+3 tiene la misma forma y orientación que el gráfico para y = 2X. Es sólo cambió tres unidades hacia la izquierda. En lugar de pasar a través de (0, 1) y (1, 2), la función desplazado pasa a través de (-3, 1) y (-2, 2). Y la gráfica de y = 2X-3 es de tres unidades a la derecha de y = 2X.
Horizontal contracción y estiramiento
Durante los siguientes dos transformaciones, ¿por qué no intenta graficar ellos por su cuenta.
Por lo tanto, cada punto de la nueva función es la mitad de su distancia original de la y-eje. los y-coordenada de cada punto sigue siendo el mismo: la X-coordinar se corta por la mitad. Por ejemplo,
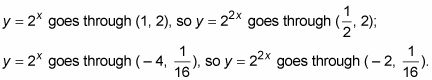
Multiplicando X por un número menor que 1 tiene el efecto opuesto.
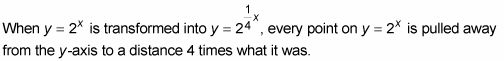
Reflexión Horizontal
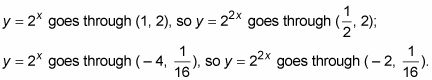
La última transformación horizontal es un reflejo sobre el y-eje.
Tenga en cuenta que después de la reflexión, los puntos están en el lado opuesto de la y-eje, pero siguen siendo la misma distancia del eje. Y los puntos originales que se encuentran en el y-eje (el y-intercepta) quedan donde están.
-
Gráficas y funciones de transformación -
¿Cómo cambiar la amplitud, período, y la posición de la tangente o gráfico cotangente -
Cómo cambiar la amplitud de un gráfico de seno o coseno -
¿Cómo combinar transformaciones con un gráfico de seno o coseno -
¿Cómo combinar varias transformaciones -
Cómo graficar y transformar una función exponencial
Cómo graficar una función racional con denominador que tiene el grado más alto Después de calcular todas las asíntotas y la X- y y-intercepciones para una función racional, que tienen toda la información que necesita para empezar a graficar la función. En cualquier función racional donde el denominador tiene un grado…
¿Cómo transformar horizontalmente gráficos padres Cuando se aplica un htransformación orizontal a un gráfico padre, usted está estirando o encogiendo el gráfico horizontalmente, a lo largo del X-eje. Un número multiplicar una variable dentro de una función afecta a la posición horizontal del…
Cómo reflejar la gráfica de una función Reflexiones tomar una función madre y proporcionar una imagen especular de la vuelta, ya sea una línea horizontal o vertical. Te encontrarás con dos tipos de reflexiones:Un número negativo se multiplica toda la función La negativa fuera de la…
Cómo cambiar un gráfico seno o coseno en el plano de coordenadas El movimiento de un seno padre o gráfica coseno alrededor del plano de coordenadas es un tipo de transformación conocido como traducción o una cambio. Para este tipo de transformación, cada punto de la gráfica de los padres se trasladó a otro…
¿Cómo traducir el gráfico de una función Al mover un gráfico horizontal o verticalmente, esto se llama un traducción. En otras palabras, cada punto de la gráfica de los padres se traduce a la izquierda, derecha, arriba o abajo. La traducción siempre implica ningún tipo de adición o…
¿Cómo transformar verticalmente una función Para transformar una función verticalmente, se agrega un número o restar un número de toda la función, o multiplica por un número. Para hacer algo para una función entera, dicenAhora, a tomar todas las transformaciones verticales mediante la…
¿Cómo transformar verticalmente gráficos padres Cuando se aplica un vertical transformación a un gráfico padre, usted está estirando o encogiendo el gráfico a lo largo del y-eje, que cambia su altura. Un número (o coeficiente) Multiplicando en frente de una función provoca la…
Ajuste del período de una función seno El período de una función de la trigonometría es la medida de la entrada de los valores que toma para que la función se ejecute a través de todos los valores posibles y empezar todo de nuevo en el mismo lugar para repetir el proceso. En el caso…
Encuentre la imagen especular de una función de la trigonometría en un gráfico Cuando multiplicas una función trigonométrica de un número negativo, todos los valores de salida se invierten en la señal. Los valores positivos se vuelven negativos y los valores negativos se convierten en positivos. El efecto que esta…
Graficar una función seno usando amplitud La función seno y cualquiera de sus variaciones tienen dos características importantes: la amplitud y periodo de la curva. Puede determinar estas características examinado sea la gráfica de la función o su ecuación.los amplitud de la función…
Funciones Gráfico tangentes con multiplicadores variables En trigonometría, multiplicando el ángulo variable en una función tangente tiene el mismo efecto como lo hace con funciones seno y coseno - que afecta el periodo de la función. Si el múltiplo es 2, como en y = Tan 2X, a continuación, la…
Como reflejo de las funciones de forma vertical u horizontal Hay dos tipos de transformaciones actúan como reflejos o volteretas. Una transformación cambia todas las salidas positivas a las salidas negativas negativos y todos a positivo. La otra invierte los insumos - positivas a negativo y negativo a…