Normas de identidad y cuantificador para la lógica cuantificador
Lógica cuantificador abarca las reglas de la lógica proposicional y se expande sobre ellos para que pueda escribir declaraciones enteras con símbolos lógicos. Esos símbolos entran en juego cuando se trabaja con identidades, o constantes intercambiables. Las reglas de la identidad se muestran aquí:
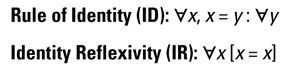
Y, cuando se habla de identidades, puede cuantificar declaraciones, usando las reglas en la tabla siguiente:
-
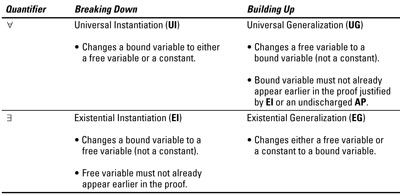
Office 2011 para Mac: actualizar manualmente una identidad comitiva a la perspectiva -
Cambio de las identidades de Outlook en Office 2011 para Mac - Cómo utilizar todos, algunos, y cualquier en sentencias SQL
-
Electrónica puertas lógicas: no puertas -
Más allá de lo básico con identidades trigonométricas -
Primeros pasos con identidades trigonométricas
¿Cómo demostrar una igualdad usando identidades co-función Identidades Co-función pueden aparecer en trig pruebas. Si usted ve la expresión pi / 2 - X paréntesis dentro de cualquier función trigonométrica, es necesario utilizar una identidad co-función para la prueba. Siga los pasos para demostrar…
¿Cómo simplificar una expresión utilizando par / impar identidades Debido seno, coseno, y la tangente son funciones (funciones trigonométricas), que pueden definirse como pares o impares funciones. Sine y la tangente son funciones impares, y el coseno es una función par. En otras palabras,pecado(-X) = -sen Xcos…
¿Cómo simplificar una expresión utilizando identidades de función co- Si usted toma la gráfica de y = Sen X y desplazar hacia la izquierda por pi / 2 unidades, se ve exactamente como la gráfica de y = Cos X. Lo mismo es cierto para la tangente y cotangente, así como secante y cosecante. Esa es la premisa básica de…
¿Cómo simplificar una expresión utilizando identidades periodicidad Identidades Periodicidad ilustrar cómo trasladar la gráfica de una función trigonométrica por un período a los resultados de izquierda o derecha en la misma función. Las funciones de seno, coseno, secante, cosecante y repetir cada 2 (pi)…
Cotangente y cosecante identidades en un círculo unitario A partir de la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, puede derivar cotangente y cosecante identidades pitagóricas. Todo lo que hacemos es tirar un poco de álgebra y aplicar las identidades recíprocas y de relación y -…
Cómo eliminar un tercer ángulo para resolver una identidad trigonometría Identidades de suma y diferencia por lo general implican dos ángulos diferentes y luego un tercer ángulo combinado. Al probar estas identidades trigonométricas, a menudo es necesario deshacerse de ese tercer ángulo. El siguiente ejemplo trata de…
Cómo cuadrar ambas partes para resolver un problema de identidad trigonometría Cuando se trabaja en ambos lados de una identidad trigonométrica, al mismo tiempo, es posible que a veces tenga que cuadrar ambos lados. Por lo general, utilizar esta técnica cuando un lado o el otro (o ambos) tiene un radical. Este método…
Identidades de producto a suma Las identidades trigonométricas de producto a suma se parecen mucho. Hay que prestar mucha atención a las diferencias sutiles para que pueda aplicarlas correctamente. A pesar de que el producto se ve bonito y compacto, que no siempre es tan fácil…
Identidades recíprocas Una gran ventaja de expresiones trigonométricas y ecuaciones es que se puede ajustar en tantas formas que se adaptan a sus necesidades. Las identidades recíprocas básicos aquí son los que la gente usa más frecuentemente.Echa un vistazo a la…
Identidades de suma a producto La suma de identidades de productos son útiles para modelar lo que ocurre con las frecuencias de sonido. Piensa en dos tonos diferentes representados por curvas sinusoidales. Añadir juntos, y ellos golpearon el uno contra el otro con un gorjeo -…
Tangente y las identidades secantes en un círculo unitario A partir de la identidad de Pitágoras, el pecado2theta- + cos2theta- = 1, puede derivar tangente y las identidades pitagóricas secantes. Todo lo que hacemos es tirar un poco de álgebra y aplicar las identidades recíprocas y de relación y -…
Lógica para dummies Trabajar con la lógica proposicional significa trabajar con un lenguaje diseñado para expresar argumentos lógicos con precisión y claridad. Para hacer uso de este lenguaje de la lógica, lo que necesita saber lo que los operadores utilicen, las…