Congruencia y semejanza en la geometría núcleo común
En matemáticas, hay muchos tipos de igualdad. En geometría básico común, los estudiantes de octavo grado estudian congruencia y similitud como dos formas de hablar sobre cómo dos formas son las mismas.
Dos formas son congruente si se puede mover una forma que se adapta perfectamente a la otra sin estirar o deformarlo. Dos formas son similar si se puede hacer lo mismo, excepto que se le permite estirar o encoger las formas proporcionalmente - usted puede duplicar todas las longitudes en una de las formas, por ejemplo.
Octavo grado necesitan especificar cuidadosamente el tamaño de la rotación (medida en grados o en fracciones de una vuelta completa) y la distancia de la corredera (medido en las unidades lineales, tales como pulgadas o centímetros) necesario para mover una forma para que partidos con una congruentes. También tienen que identificar con precisión el factor por el cual necesita una forma de ser estirado o encogido de igualar una forma similar.
Por ejemplo, mirar a la figura y determinar cuales son los mismos.
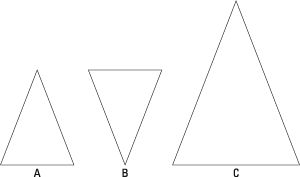
En este ejemplo, sólo triángulos A y B son congruentes. Pero triángulo C es similar tanto para A y B. Así que las formas son la mismo? Depende de lo que entiendas por igual. Esta confusión es por qué los matemáticos usan las palabras congruente y similar - los significados de estas palabras son mucho más preciso que el significado de mismo.
-
Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 2 - Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 8
- Las normas fundamentales comunes: conceptos matemáticos que su hijo debe aprender en el grado 4
-
Conceptos de geometría a su estudiante de la escuela secundaria deben conocer las normas básicas comunes -
Alta trig escolar en matemáticas núcleo común -
Cómo núcleo común matemática define las líneas y ángulos
Cómo rotación ángulos se miden en la geometría núcleo común En geometría básico común, de cuarto grado trabajan con fracciones de una rotación completa - mitades, cuartos, y así sucesivamente. También trabajan con medición de ángulos en grados, en un grado esde una rotación completa. Utilizan…
Matemáticas normas fundamentales comunes: similitud, triángulos rectángulos, y trigonometría Las normas esenciales comunes en este grupo se centran principalmente en triángulos. Los estudiantes descubren el concepto de similitud y la escala y explorar cómo estos conceptos se aplican a situaciones del mundo real. La naturaleza única de…
Formas de partición utilizando conjuntos en matemáticas núcleo común En Common Core matemáticas, los estudiantes de segundo grado aprenden a dibujar formas en función de sus propiedades. También utilizan matrices para dividir o cortar, estas formas.Los estudiantes aprenden a imaginar formas que tienen conjuntos…
Fórmulas para formas geométricas comunes Dependiendo del problema de álgebra, usted necesita saber algo de geometría. Lo siguiente representa algunas de las formas más comunes en la geometría y sus fórmulas de perímetro, área, volumen, superficies, y la circunferencia:…
La clasificación de tres tipos de triángulos Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos. Es decir, un triángulo tiene tres lados, y tres términos…
Libro de Geometría para dummies Si estás estudiando geometría, que se está viendo en todas partes símbolos - símbolos de arcos y ángulos, líneas y triángulos, así como símbolos de las relaciones entre las líneas y ángulos y así sucesivamente. A continuación se…
Cómo medir segmentos de línea Para encontrar la medida o el tamaño de un segmento, sólo tiene que medir su longitud. ¿Qué más se puede medir? Después de todo, la longitud es la única característica tiene un segmento. Tienes tu resumen, su medio y sus segmentos largos.…
¿Cómo demostrar triángulos semejantes con sas ~ Usted puede probar que los triángulos son similares utilizando el método SAS ~ (Side-Angle-Side). SAS ~ establece que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo y los ángulos incluidos son congruentes,…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
¿Cómo demostrar triángulos semejantes con sss ~ Usted puede probar que los triángulos son similares utilizando el método SSS ~ (Side-Side-Side). SSS ~ establece que si las relaciones de los tres pares de lados de dos triángulos correspondientes son iguales, entonces los triángulos son…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
Formas y pruebas de aritmética Muchas pruebas de aritmética le piden que describa las formas de alguna manera. ¡Tienes que ser capaz de identificar diferentes formas y el número de lados de cada forma tiene.Encontrar el ánguloLos ángulos se miden en grados. Por ejemplo, si…